
����Ŀ��Ϊ�ٽ��¾ɹ���ת������߾���Ч�棬ij�Ƽ���˾�����з���һ�����߿Ƽ��豸��ÿ̨�豸�ɱ���Ϊ25��Ԫ�������г����з��֣����豸����������![]() ��̨�������۵���
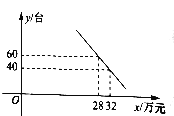
��̨�������۵���![]() ����Ԫ��������ͼ��ʾ��һ�κ�����ϵ��
����Ԫ��������ͼ��ʾ��һ�κ�����ϵ��
��1������������![]() �����۵���
�����۵���![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2��������ع涨�����豸�����۵��۲��ø���35��Ԫ������ù�˾����130��Ԫ����������ô���豸�����۵���Ӧ�Ƕ�����Ԫ��
���𰸡���1��![]() ��
��![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ����2�����豸�����۵���Ӧ��27 ��Ԫ��
����2�����豸�����۵���Ӧ��27 ��Ԫ��
��������
��1������ͼ���ϵ�����![]() ,����
,����![]() ,�ô���ϵ�����������.
,�ô���ϵ�����������.
��2������������=��������![]() �������г����̼���.
�������г����̼���.
�⣺��1����![]() ��
��![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��
��
�����⣬��![]() ���
���![]()
����![]() ��
��![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��
��
��2������֪![]() ��
��
�������̣���![]() ��
��
���![]() ��
��
�ߴ��豸�����۵��۲��ø���35��Ԫ��
��![]() ���ᣩ������
���ᣩ������![]() ��
��
�𣺸��豸�����۵���Ӧ��27 ��Ԫ��


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ�����μ�У�˶��ᣬ������5����Ŀ�ɹ�ѡ������Ŀ��100m��200m��![]() �ֱ���
�ֱ���![]() ��
��![]() ��
��![]() ��ʾ
��ʾ![]() ��������Ŀ����Զ������
��������Ŀ����Զ������![]() �ֱ���
�ֱ���![]() ��
��![]() ��ʾ
��ʾ![]() ��
��
![]() ��ͬѧ��5����Ŀ����ѡһ����ǡ����������Ŀ�ĸ���Ϊ______��
��ͬѧ��5����Ŀ����ѡһ����ǡ����������Ŀ�ĸ���Ϊ______��
![]() ��ͬѧ��5����Ŀ����ѡ������������״ͼ������оٳ����п��ܳ��ֵĽ��������ǡ����һ��������Ŀ��һ��������Ŀ�ĸ��ʣ�
��ͬѧ��5����Ŀ����ѡ������������״ͼ������оٳ����п��ܳ��ֵĽ��������ǡ����һ��������Ŀ��һ��������Ŀ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
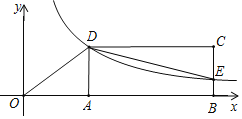
����Ŀ����ͼ������ABCD�Ķ���A��B��x����������ϣ�����������y=![]() �ڵ�һ�����ڵ�ͼ����ֱ��y=
�ڵ�һ�����ڵ�ͼ����ֱ��y=![]() x���ڵ�D���ҷ���������y=
x���ڵ�D���ҷ���������y=![]() ��BC�ڵ�E��AD=3��
��BC�ڵ�E��AD=3��
��1����D������꼰�����������Ĺ�ϵʽ��
��2�������ε������24����д����CDE�����������Ҫд�����̣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪������y=��x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��y�ύ��C�㣬��P�����������ڵ�һ�����ڵ�һ�����㣬�ҵ�P�ĺ�����Ϊt��
��1���������ߵı���ʽ��
��2���������ߵĶԳ���Ϊl��l��x��Ľ���ΪD����ֱ��l���Ƿ���ڵ�M��ʹ���ı���CDPM��ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2������BC��PB��PC������PBC�����ΪS��
����S����t�ĺ�������ʽ��
����P�㵽ֱ��BC�ľ�������ֵ���������ʱ��P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����С����Χ��һ��������������������һ�߿�ǽ�����������ó�Ϊ30�����Χ�ɡ���֪ǽ��Ϊ18��(��ͼ��ʾ)�������������ֱ��ǽ��һ�ߵij�Ϊx��.

(1)��ƽ����ǽ��һ�߳�Ϊy�ף�ֱ��д��y��x�ĺ�����ϵʽ�����Ա���x��ȡֵ��Χ.
(2)��ֱ��ǽ��һ�ߵij�Ϊ������ʱ��������������������������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC�Ĵ�ֱƽ����EF�ֱ�BC��AD�ڵ�E��F����BE=3��AF=5����AC�ij�Ϊ�� ��

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��.��֪���ھ���![]() �У�
�У�![]() �ǶԽ��ߣ�
�ǶԽ��ߣ�![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��

��1����ͼ1����֤��![]() ��
��
��2����ͼ2����![]() ʱ������
ʱ������![]() .
.![]() ���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2���ĸ������Σ�ʹд����ÿ�������ε���������ھ���
���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2���ĸ������Σ�ʹд����ÿ�������ε���������ھ���![]() �����
�����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɽ������������ĸ�ɽ����������λ���żҽ�����ɽ��������һ�μ���ά���У�������Ա������A����ʼ����A��B��C·�߶��������м���ά������ͼ����֪![]() �ף�
�ף�![]() �ף�AB��ˮƽ��
�ף�AB��ˮƽ��![]() �ļн���
�ļн���![]() ��BC��ˮƽ��
��BC��ˮƽ��![]() �ļн���
�ļн���![]() �����μ����У�������Ա�����Ĵ�ֱ�߶�
�����μ����У�������Ա�����Ĵ�ֱ�߶�![]() �Ƕ����ף�(�����ȷ��1�ף��ο����ݣ�
�Ƕ����ף�(�����ȷ��1�ף��ο����ݣ�![]() )
)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�AB=AC����ABΪֱ������O���ֱ�BC�ڵ�D����CA���ӳ����ڵ�E������D��
�У�AB=AC����ABΪֱ������O���ֱ�BC�ڵ�D����CA���ӳ����ڵ�E������D��![]() �ڵ�H������DE���߶�OA�ڵ�F��
�ڵ�H������DE���߶�OA�ڵ�F��
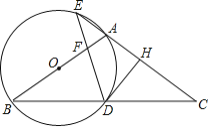
��1���Բ���ֱ��DH���O��λ�ù�ϵ����˵�����ɣ�
��2����AE=AH��EF=4����DF��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com