
科目: 来源: 题型:
【题目】如图,已知:抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D为顶点,连接BD,CD,抛物线的对称轴与x轴交与点E.
(1)求抛物线解析式及点D的坐标;
(2)G是抛物线上B,D之间的一点,且S四边形CDGB=4S△DGB,求出G点坐标;
(3)在抛物线上B,D之间是否存在一点M,过点M作MN⊥CD,交直线CD于点N,使以C,M,N为顶点的三角形与△BDE相似?若存在,求出满足条件的点M的坐标,若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】天府新区某校数学活动小组在一次活动中,对一个数学问题作如下探究:
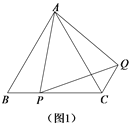
(1)问题发现:如图1,在等边△ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ.求证:BP CQ;
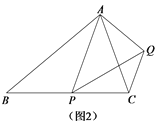
(2)变式探究:如图2,在等腰△ABC中,ABBC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP PQ,APQ ABC,连接CQ.判断∠ABC和∠ACQ的数量关系,并说明理由;
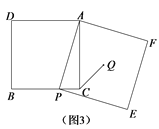
(3)解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形 APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为6,![]() ,求正方形ADBC的边长.
,求正方形ADBC的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,当m,n满足mn=k(k为常数,且m>0,n>0)时,就称点(m,n)为“等积点”.若直线y=﹣x+b(b>0)与x轴、y轴分别交于点A和点B,并且该直线上有且只有一个“等积点”,过点A与y轴平行的直线和过点B与x轴平行的直线交于点C,点E是直线AC上的“等积点”,点F是直线BC上的“等积点”,若△OEF的面积为![]() ,则OE=______.
,则OE=______.
查看答案和解析>>
科目: 来源: 题型:
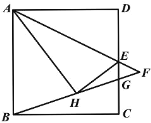
【题目】如图,在正方形ABCD中,AB=2,点E是CD的中点,连接AE,将△ADE沿AE折叠至△AHE,连接BH,延长AE,BH交于点F;BF,CD交于点G,则FG=_______.
查看答案和解析>>
科目: 来源: 题型:
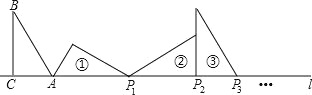
【题目】如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() ;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0..其中正确的结论有:
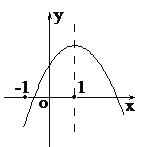
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知抛物线y=x2+mx+m﹣1的顶点为D,交y轴于C点,交x轴于A(x1,0),B(x2,0)两点,点A在y轴左边,点B在y轴右边,且AB=4.
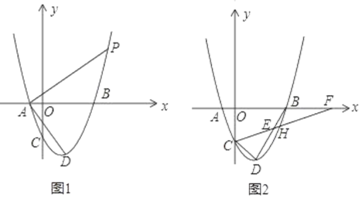
(1)求抛物线的解析式;
(2)如图1,AP⊥AD交抛物线于P.求点P的坐标;
(3)如图2,点H为B,D之间抛物线上一点,直线CH交BD于E,交x轴于F,若S△CDE=S△BEF,求H点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC与△ADE都是等腰直角三角形,且AC=AB,AD=AE,连接DC,点M、P、N分别为DE、DC、BC的中点.

(1)如图1,当点D、E分别在边AB、AC上,线段PM与PN的数量关系是 ,位置关系是 ;
(2)把等腰Rt△ADE绕点A旋转到如图2的位置,连接MN,判断△PMN的形状,并说明理由;
(3)把等腰Rt△ADE绕点A在平面内任意旋转,AD=2,AB=6,请直接写出△PMN的面积S的变化范围 .
查看答案和解析>>
科目: 来源: 题型:
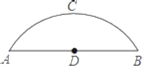
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com