
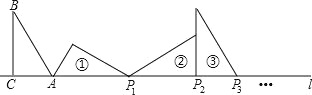
����Ŀ����ͼRt��ABC�У���ACB��90������B��30����AC��1����AC��ֱ��l�ϣ�����ABC�Ƶ�A˳ʱ����ת���٣��ɵõ���P1����ʱAP1��2����λ�âٵ��������Ƶ�P1˳ʱ����ת��λ�âڣ��ɵõ���P2����ʱAP2��2+![]() ����λ�âڵ��������Ƶ�P2˳ʱ����ת��λ�âۣ��ɵõ���P3����ʱAP3��3+
����λ�âڵ��������Ƶ�P2˳ʱ����ת��λ�âۣ��ɵõ���P3����ʱAP3��3+![]() �������˹��ɼ�����ת��ֱ����P2020Ϊֹ����AP2020����_______��
�������˹��ɼ�����ת��ֱ����P2020Ϊֹ����AP2020����_______��
���𰸡�![]()
��������
�������⣬���ֽ�Rt��ABC�Ƶ�A˳ʱ����ת��ÿ��תһ�Σ�AP�ij�����������2��![]() ��1��������һѭ�������˹��ɼ�����⣮
��1��������һѭ�������˹��ɼ�����⣮
�⣺�ߡ�ACB��90������B��30����AC��1��
��AB��2��BC��![]() ��
��
�ཫRt��ABC�Ƶ�A˳ʱ����ת��ÿ��תһ�Σ�AP�ij�����������2��![]() ��1��������һѭ����
��1��������һѭ����
��2020��3��673��1��
��AP2020��673��2��![]() ��1����2��2021��673
��1����2��2021��673![]() ��
��
�ʴ�Ϊ��2021��673![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
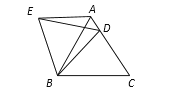
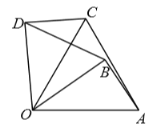
����Ŀ���ڵȱ���ABC�У�D�DZ�AC��һ�㣬����BD������BCD�Ƶ�B��ʱ����ת60�����õ���BAE������ED����BC=8��BD=6���������ĸ����ۣ��١�AEB=��BDC����AE��BC���ۡ�BDE�ǵȱ������Σ��ܡ�ADE���ܳ���14��������ȷ�Ľ�����_____��������Ϊ��ȷ���۵���Ŷ����ϣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
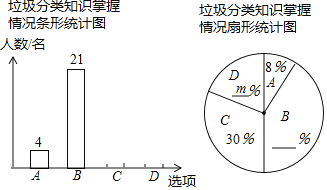
����Ŀ��Ϊ��Ӧ���������ڡ����������![]() �������������������������֣���������ѧ��������˲���ѧ������������֪ʶ���������������ѡ���Ϊ��A���dz��˽⣻B���Ƚ��˽⣻C���˽���٣�D�����˽�
�������������������������֣���������ѧ��������˲���ѧ������������֪ʶ���������������ѡ���Ϊ��A���dz��˽⣻B���Ƚ��˽⣻C���˽���٣�D�����˽�![]() �����֣��������������Ƴ�����������������ͳ��ͼ
�����֣��������������Ƴ�����������������ͳ��ͼ![]() �����ͼ���ṩ����Ϣ������������⣻
�����ͼ���ṩ����Ϣ������������⣻
![]() ��
��![]() ______������ȫ����ͳ��ͼ��
______������ȫ����ͳ��ͼ��
![]() ����Уѧ������Ϊ1000�������ݵ����������Ƹ�У���dz��˽⡱�롰�Ƚ��˽⡱��ѧ������______����
����Уѧ������Ϊ1000�������ݵ����������Ƹ�У���dz��˽⡱�롰�Ƚ��˽⡱��ѧ������______����
![]() ��֪���dz��˽⡱����3��������1��Ů�������������ȡ2����ȫУ�����������֪ʶ�������뻭��״ͼ���б��ķ�������ǡ�ó鵽1��1Ů�ĸ��ʣ�
��֪���dz��˽⡱����3��������1��Ů�������������ȡ2����ȫУ�����������֪ʶ�������뻭��״ͼ���б��ķ�������ǡ�ó鵽1��1Ů�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�ǵ���ֱ�������Σ���BAC�� 90����AB��AC���ı���ADEF�������Σ���B��C�ֱ��ڱ�AD��AF�ϣ���ʱBD��CF��BD��CF������

��1������ABC�Ƶ�A��ʱ����ת����0��������90����ʱ����ͼ2��BD��CF����������������֤����������������˵�����ɣ�
��2������ABC�Ƶ�A��ʱ����ת45��ʱ����ͼ3���ӳ�DB��CF�ڵ�H.
����֤��BD��CF��
����AB��2��AD��3![]() ʱ�����߶�DH�ij���
ʱ�����߶�DH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
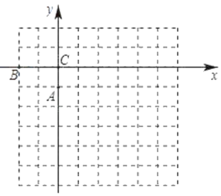
����Ŀ����ͼ��ƽ��ֱ������ϵ�У��Ե�CΪ����ԭ�㣬��A(0����1)��B(��2��0)������ABC�Ƶ�A˳ʱ����ת90����
��1����ͼ�л�����ת�����AB��C������д����B����C�������ꣻ
��2����֪��D(3����2)����x��������һ��P��ע����Ҫ��д��P������꣩��ʹ��PC��+PD��ֵ��С�������PC��+PD����Сֵ��
��3��д����ABC����ת�����У��߶�ABɨ��������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������y��x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C����DΪ���㣬����BD��CD�������ߵĶԳ�����x�ύ���E��
��1���������߽���ʽ����D�����ꣻ
��2��G����������B��D֮���һ�㣬��S�ı���CDGB��4S��DGB�����G�����ꣻ
��3������������B��D֮���Ƿ����һ��M������M��MN��CD����ֱ��CD�ڵ�N��ʹ��C��M��NΪ��������������BDE���ƣ������ڣ�������������ĵ�M�����꣬�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ϲ��ֵ�ĺ�����
�ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ���±���
�Ķ�Ӧֵ���±���
![]()
���ϱ���֪������˵������ȷ���ǣ� �� (��д���)
����������![]() ���һ������Ϊ
���һ������Ϊ![]()
�ں���![]() �����ֵΪ6
�����ֵΪ6
�������ߵĶԳ�����ֱ��![]() ��
��
���ڶԳ�����࣬ ![]() ��
��![]() ���������
���������
A.�٢ڢ�B.�٢ڢ�C.�٢ڢۢ�D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ����ʱ����ת
����ʱ����ת![]() �õ�
�õ�![]() ����
����![]() ��
��![]() �������н��۲�һ����ȷ���ǣ� ��
�������н��۲�һ����ȷ���ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PAΪ��O�����ߣ�PB���O����B��C���㣬��֪PA��6��PB��3����PC��_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com