
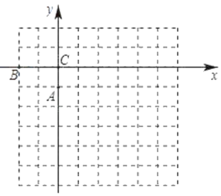
【题目】如图,平面直角坐标系中,以点C为坐标原点,点A(0,﹣1),B(﹣2,0),将△ABC绕点A顺时针旋转90°.
(1)在图中画出旋转后的△AB′C′,并写出点B′、C′的坐标;
(2)已知点D(3,﹣2),在x轴上求作一点P(注:不要求写出P点的坐标),使得PC′+PD的值最小,并求出PC′+PD的最小值;
(3)写出△ABC在旋转过程中,线段AB扫过的面积 .
【答案】(1)见解析,(1,1)和(1,﹣1);(2)见解析,![]() ;(3)
;(3)![]()
【解析】
(1)依据△ABC绕点A顺时针旋转90°,即可得到旋转后的△AB′C′,并写出点B′、C′的坐标;
(2)点B'与点C'关于x轴对称,连接B'D交x轴于点P,则PC′+PD的值最小,依据勾股定理即可得到PC′+PD的最小值;
(3)依据扇形的面积计算公式,即可得到线段AB扫过的面积.
解:(1)如图所示,△AB′C′即为所求,点B′、C′的坐标分别为(1,1)和(1,﹣1);

(2)如图所示,点B'与点C'关于x轴对称,连接B'D交x轴于点P,则PC′+PD的值最小,
PC′+PD的最小值为![]() ;
;
(3)线段AB扫过的面积为:![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
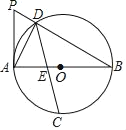
【题目】如图,AB为⊙O的直径,且AB=m(m为常数),点C为![]() 的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
(1)当DC⊥AB时,则![]() = ;
= ;
(2)①当点D在![]() 上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
②设CD长为t,求△ADB的面积S与t的函数关系式;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
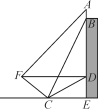
【题目】如图,光明中学一教学楼顶上竖有一块高为AB的宣传牌,点E和点D分别是教学楼底部和外墙上的一点(A,B,D,E在同一直线上),小红同学在距E点9米的C处测得宣传牌底部点B的仰角为67°,同时测得教学楼外墙外点D的仰角为30°,从点C沿坡度为1∶![]() 的斜坡向上走到点F时,DF正好与水平线CE平行.
的斜坡向上走到点F时,DF正好与水平线CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若在点F处测得宣传牌顶部A的仰角为45°,求出宣传牌AB的高度(结果精确到0.01).(注:sin67°≈0.92,tan67°≈2.36,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
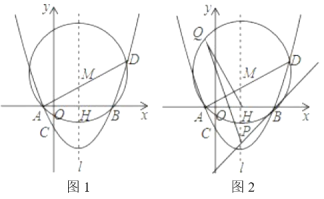
【题目】如图1,在平面直角坐标系中,抛物线y![]() x2bxc交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).
x2bxc交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).
(1)求此抛物线的解析式;
(2)在抛物线上取点D,若点D的横坐标为5,求点D的坐标及∠ADB的度数;
(3)在(2)的条件下,设抛物线对称轴![]() 交x轴于点H,△ABD的外接圆圆心为M(如图1),
交x轴于点H,△ABD的外接圆圆心为M(如图1),
①求点M的坐标及⊙M的半径;
②过点B作⊙M的切线交![]() 于点P(如图2),设Q为⊙M上一动点,则在点Q运动过程中
于点P(如图2),设Q为⊙M上一动点,则在点Q运动过程中![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
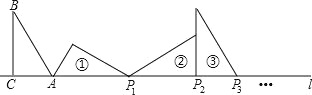
【题目】如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() ;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
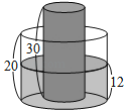
【题目】如图,有一内部装有水的直圆柱形水桶,桶高![]() ;另有一直圆柱形的实心铁柱,柱高
;另有一直圆柱形的实心铁柱,柱高![]() ,直立放置于水桶底面上,水桶内的水面高度为
,直立放置于水桶底面上,水桶内的水面高度为![]() ,且水桶与铁柱的底面半径比为
,且水桶与铁柱的底面半径比为![]() .今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为( )
.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).
(1)先将Rt△ABC向右平移5个单位,再向下平移1个单位后得到Rt△A1B1C1.试在图中画出图形Rt△A1B1C1,并写出A1的坐标;
(2)将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出图形Rt△A2B2C2.并计算Rt△A1B1C1在上述旋转过程中C1所经过的路程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com