
【题目】如图,将![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 得到
得到![]() ,若
,若![]() ,
,![]() ,则下列结论不一定正确的是( )
,则下列结论不一定正确的是( )
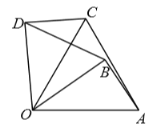
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】 已知四边形ABCD的是边长为4的正方形,AC为对角线,将△ACD绕点A逆时针旋转45度,得到△AEF(其中点D的对应点是点F,点C的对应点是点E),则线段CF的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
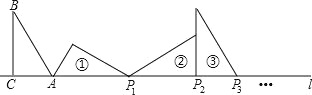
【题目】如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() ;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一内部装有水的直圆柱形水桶,桶高![]() ;另有一直圆柱形的实心铁柱,柱高
;另有一直圆柱形的实心铁柱,柱高![]() ,直立放置于水桶底面上,水桶内的水面高度为
,直立放置于水桶底面上,水桶内的水面高度为![]() ,且水桶与铁柱的底面半径比为
,且水桶与铁柱的底面半径比为![]() .今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为( )
.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为( )
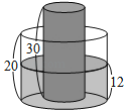
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点
的顶点![]() 在
在![]() 轴上.
轴上.
(1)若点![]() 是抛物线最低点,且落在
是抛物线最低点,且落在![]() 轴正半轴上,直接写出
轴正半轴上,直接写出![]() 的取值范围;
的取值范围;
(2)![]() ,
,![]() 是抛物线上两点,若
是抛物线上两点,若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,且当
,且当![]() 的绝对值为4时,
的绝对值为4时,![]() 为等腰直角三角形(其中
为等腰直角三角形(其中![]() ).
).
①求抛物线的解析式;
②设![]() 中点为
中点为![]() ,若
,若![]() ,求点
,求点![]() 纵坐标的最小值.
纵坐标的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大黄鱼是中国特有的地方性鱼类,有“国鱼”之称,由于过去滥捕等多种因素,大黄鱼资源已基本枯竭,目前,我市已培育出十余种大黄鱼品种,某鱼苗人工养殖基地对其中的四个品种“宁港”、“御龙”、“甬岱”、“象山港”共300尾鱼苗进行成活实验,从中选出成活率最高的品种进行推广,通过实验得知“甬岱”品种鱼苗成活率为![]() ,并把实验数据绘制成下列两幅统计图(部分信息未给出):
,并把实验数据绘制成下列两幅统计图(部分信息未给出):
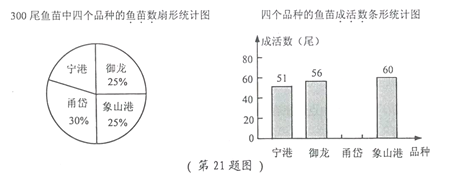
(1) 求实验中“宁港”品种鱼苗的数量;
(2) 求实验中“甬岱”品种鱼苗的成活数,并补全条形统计图;
(3)你认为应选哪一品种进行推广?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
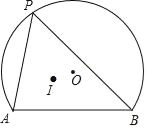
【题目】如图,AB为弓形AB的弦,AB=2![]() ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com