
【题目】 已知四边形ABCD的是边长为4的正方形,AC为对角线,将△ACD绕点A逆时针旋转45度,得到△AEF(其中点D的对应点是点F,点C的对应点是点E),则线段CF的长是______.
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
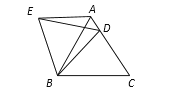
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=8,BD=6.则下列四个结论:①∠AEB=∠BDC;②AE∥BC;③△BDE是等边三角形;④△ADE的周长是14.其中正确的结论是_____(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步改善路容路貌,提升干线公路美化度,某地相关部门初步拟定派一个工程队对一段长度不少于39000米的公路进行路基标准化整修.该工程队以旧设备与新设备交替使用的方式施工,原计划旧设备每小时整修公路30米,新设备每小时整修公路60米
(1)出于保护旧设备的目的,该工程队计划使用新设备的时间比使用旧设备的时间多![]() ,当这个工程完工时,旧设备的使用时间至少为多少小时?
,当这个工程完工时,旧设备的使用时间至少为多少小时?
(2)通过精确的勘察、测测量、规划,以及新增了部分支线公路整修,此工程的实际施工里程比最初拟定的最少里程39000米多了9000米,于是在实际施工中,旧设备在整修公路效率不变的情况下,使用时间比(1)中的最小值多![]() ,同时,因为工人操作新设备不够熟练,使得得新设备整修公路的效率比原计划下降了
,同时,因为工人操作新设备不够熟练,使得得新设备整修公路的效率比原计划下降了![]() ,使用时间比(1)中新设备使用的最短时间多
,使用时间比(1)中新设备使用的最短时间多![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 爱好数学的甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字-1,0,1且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为p的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为q值,两次结果记为(p,q).
(1)请你帮他们用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
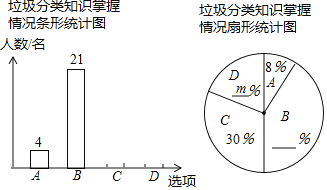
【题目】为响应市政府关于“垃圾不落地![]() 市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解
市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解![]() ”四种,并将调查结果绘制成以下两幅不完整的统计图
”四种,并将调查结果绘制成以下两幅不完整的统计图![]() 请根据图中提供的信息,解答下列问题;
请根据图中提供的信息,解答下列问题;
![]() 求
求![]() ______,并补全条形统计图;
______,并补全条形统计图;
![]() 若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
![]() 已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com