
����Ŀ��Ϊ��һ������·��·ò���������߹�·�����ȣ�ij����ز��ų����ⶨ��һ�����̶Ӷ�һ�γ��Ȳ�����39000�Ĺ�·����·���������ޣ��ù��̶��Ծ��豸�����豸����ʹ�õķ�ʽʩ����ԭ�ƻ����豸ÿСʱ����·30�ף����豸ÿСʱ����·60��
��1�����ڱ������豸��Ŀ�ģ��ù��̶Ӽƻ�ʹ�����豸��ʱ���ʹ�þ��豸��ʱ���![]() ������������깤ʱ�����豸��ʹ��ʱ������Ϊ����Сʱ��
������������깤ʱ�����豸��ʹ��ʱ������Ϊ����Сʱ��
��2��ͨ����ȷ�Ŀ��졢��������滮���Լ������˲���֧�߹�·���ޣ��˹��̵�ʵ��ʩ����̱�����ⶨ���������39000����9000�ף�������ʵ��ʩ���У����豸������·Ч�ʲ��������£�ʹ��ʱ��ȣ�1���е���Сֵ��![]() ��ͬʱ����Ϊ���˲������豸����������ʹ�õ����豸����·��Ч�ʱ�ԭ�ƻ��½���
��ͬʱ����Ϊ���˲������豸����������ʹ�õ����豸����·��Ч�ʱ�ԭ�ƻ��½���![]() ��ʹ��ʱ��ȣ�1�������豸ʹ�õ����ʱ���
��ʹ��ʱ��ȣ�1�������豸ʹ�õ����ʱ���![]() ����
����![]() ��ֵ��
��ֵ��
���𰸡���1��300 ��2��32
��������
��1��������������깤ʱ���豸��ʹ��ʱ������ΪxСʱ�����������ҵ����������ϵ��ʹ�����豸���Ĺ�·������ʹ�þ��豸���Ĺ�·�����ĺͲ�����39000�ף��г�����ʽ���ⲻ��ʽ���ɣ�
��2�����������֪����ʵ��ʩ����ʹ�þ��豸��ʱ��Ϊ300��(1+3.2![]() %)Сʱ��ÿСʱ����·30�ף�ʹ�����豸��ʱ��Ϊ300
%)Сʱ��ÿСʱ����·30�ף�ʹ�����豸��ʱ��Ϊ300![]() (1-
(1-![]()
![]() %-30%)Сʱ��ÿСʱ����·60��(1-
%-30%)Сʱ��ÿСʱ����·60��(1-![]() %)�ף���ʵ��ʩ����ʹ�����豸���Ĺ�·����Ϊ300��(1+3.2
%)�ף���ʵ��ʩ����ʹ�����豸���Ĺ�·����Ϊ300��(1+3.2![]() %)��30����ʹ�þ��豸��������60��(1-
%)��30����ʹ�þ��豸��������60��(1-![]() %)��300
%)��300![]() (1-
(1-![]()
![]() %-30%)��������·�����������������������ϵ�г����̣�����⼴�ɣ�
%-30%)��������·�����������������������ϵ�г����̣�����⼴�ɣ�
�⣺����������깤ʱ�����豸��ʹ��ʱ������ΪxСʱ,�����豸��ʹ��ʱ��Ϊ![]() Сʱ�����������
Сʱ�����������
![]()
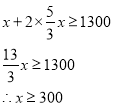
�𣺵���������깤ʱ�����豸��ʹ��ʱ������Ϊ300Сʱ
��2���������
300��(1+3.2![]() %)��30+60��(1-
%)��30+60��(1-![]() %)��300
%)��300![]() �� (1+
�� (1+![]()
![]() %+30%)=39000+9000
%+30%)=39000+9000
ԭ���̻����![]()
���![]() ��
��![]() ��
��
��![]() ��0
��0
��![]() =
=![]()
��![]() ��ֵ��
��ֵ��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
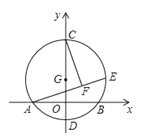
����Ŀ����ͼ����G(0��3)ΪԲ�ģ��뾶Ϊ6��Բ��x�ύ��A��B���㣬��y�ύ��C��D���㣬��EΪ��G��һ���㣬CF��AE��F����E����G���˶������У��߶�FG�ij��ȵ���СֵΪ(����)
A.![]() 1B.2
1B.2![]() -2C.3
-2C.3![]() D.3
D.3![]() 3
3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
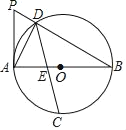
����Ŀ����ͼ��ABΪ��O��ֱ������AB��m��mΪ����������CΪ![]() ���е㣬��DΪԲ��һ���㣬��A������O�����߽�BD���ӳ����ڵ�P����CD��AB�ڵ�E��
���е㣬��DΪԲ��һ���㣬��A������O�����߽�BD���ӳ����ڵ�P����CD��AB�ڵ�E��
��1����DC��ABʱ����![]() ���� ����
���� ����
��2���ٵ���D��![]() ���ƶ�ʱ����̽���߶�DA��DB��DC֮���������ϵ����˵�����ɣ�
���ƶ�ʱ����̽���߶�DA��DB��DC֮���������ϵ����˵�����ɣ�
����CD��Ϊt�����ADB�����S��t�ĺ�����ϵʽ��
��3����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ij���۹��������ص�EΪ�ļ���Ŀ��������.��֪��E������������AB�ľ���OEΪ10��,����ABΪ123��(AB��ֱ����BC),�ڵ���C����õ�E�����Ǧ�=45��,�ӵ�C��CB����ǰ��40����D��,��D���������A�����Ǧ�=60��,���E�����ĸ߶�EF.(�����ȷ��0.1��)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ�
��abc��0����b��a+c����4a+2b+c��0����2c��3b����a+b��m��am+b����m��1��ʵ������
������ȷ�Ľ����У�������
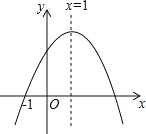
A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
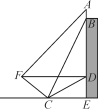
����Ŀ�� ��֪�ı���ABCD���DZ߳�Ϊ4�������Σ�ACΪ�Խ��ߣ�����ACD�Ƶ�A��ʱ����ת45�ȣ��õ���AEF�����е�D�Ķ�Ӧ���ǵ�F����C�Ķ�Ӧ���ǵ�E�������߶�CF�ij���______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ѧһ��ѧ¥��������һ���ΪAB�������ƣ���E�͵�D�ֱ��ǽ�ѧ¥�ײ�����ǽ�ϵ�һ��(A��B��D��E��ͬһֱ����)��С��ͬѧ�ھ�E��9��C����������Ƶײ���B������Ϊ67�㣬ͬʱ��ý�ѧ¥��ǽ���D������Ϊ30�㣬�ӵ�C���¶�Ϊ1��![]() ��б�������ߵ���Fʱ��DF������ˮƽ��CEƽ�У�
��б�������ߵ���Fʱ��DF������ˮƽ��CEƽ�У�
(1)���F��ֱ��CE�ľ���(�����������)��
(2)���ڵ�F����������ƶ���A������Ϊ45�㣬���������AB�ĸ߶�(�����ȷ��0.01)��(ע��sin67���0.92��tan67���2.36��![]() ��1.41��
��1.41��![]() ��1.73)
��1.73)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
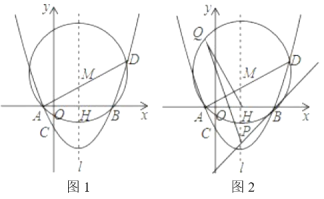
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y![]() x2bxc��x���ڵ�A��B����B������Ϊ(4��0)����y���ڽ��ڵ�C(0����2)��
x2bxc��x���ڵ�A��B����B������Ϊ(4��0)����y���ڽ��ڵ�C(0����2)��
��1����������ߵĽ���ʽ��
��2������������ȡ��D������D�ĺ�����Ϊ5�����D�����꼰��ADB�Ķ�����
��3���ڣ�2���������£��������߶Գ���![]() ��x���ڵ�H����ABD�����ԲԲ��ΪM����ͼ1����
��x���ڵ�H����ABD�����ԲԲ��ΪM����ͼ1����
�����M�����꼰��M�İ뾶��
�ڹ���B����M�����߽�![]() �ڵ�P����ͼ2������QΪ��M��һ���㣬���ڵ�Q�˶�������
�ڵ�P����ͼ2������QΪ��M��һ���㣬���ڵ�Q�˶�������![]() ��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵�����ɣ�
��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
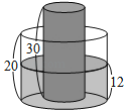
����Ŀ����ͼ����һ�ڲ�װ��ˮ��ֱԲ����ˮͰ��Ͱ��![]() ������һֱԲ���ε�ʵ������������
������һֱԲ���ε�ʵ������������![]() ��ֱ��������ˮͰ�����ϣ�ˮͰ�ڵ�ˮ��߶�Ϊ
��ֱ��������ˮͰ�����ϣ�ˮͰ�ڵ�ˮ��߶�Ϊ![]() ����ˮͰ�������ĵ���뾶��Ϊ
����ˮͰ�������ĵ���뾶��Ϊ![]() ����С�ͽ���������ˮͰ�ⲿ��������ˮͰ�ڵ�ˮ��δ�ı䣬������ˮͰ��ȣ���ˮͰ�ڵ�ˮ��߶ȱ�Ϊ�� ��
����С�ͽ���������ˮͰ�ⲿ��������ˮͰ�ڵ�ˮ��δ�ı䣬������ˮͰ��ȣ���ˮͰ�ڵ�ˮ��߶ȱ�Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com