
【题目】已知抛物线![]() 的顶点
的顶点![]() 在
在![]() 轴上.
轴上.
(1)若点![]() 是抛物线最低点,且落在
是抛物线最低点,且落在![]() 轴正半轴上,直接写出
轴正半轴上,直接写出![]() 的取值范围;
的取值范围;
(2)![]() ,
,![]() 是抛物线上两点,若
是抛物线上两点,若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,且当
,且当![]() 的绝对值为4时,
的绝对值为4时,![]() 为等腰直角三角形(其中
为等腰直角三角形(其中![]() ).
).
①求抛物线的解析式;
②设![]() 中点为
中点为![]() ,若
,若![]() ,求点
,求点![]() 纵坐标的最小值.
纵坐标的最小值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②当
;②当![]() 时,
时,![]() 最小值是2.
最小值是2.
【解析】
(1)由顶点![]() 是抛物线最低点,可判断抛物线开口向上,可判定a的符号;根据抛物线的解析式确定顶点坐标,根据顶点A落在
是抛物线最低点,可判断抛物线开口向上,可判定a的符号;根据抛物线的解析式确定顶点坐标,根据顶点A落在![]() 轴正半轴上,可判定h、k的取值范围;
轴正半轴上,可判定h、k的取值范围;
(2)①由已知可得当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,所以对称轴为![]() 轴,即可确定抛物线为y=ax2,再由△APQ为等腰直角三角形和y1的绝对值为4,得到a=
轴,即可确定抛物线为y=ax2,再由△APQ为等腰直角三角形和y1的绝对值为4,得到a=![]() ;
;
②设N点坐标为(x,y),PQ2=8y+4y2-![]() (x1x2+4)2+4≥36,所以4(y+1)2≥36+
(x1x2+4)2+4≥36,所以4(y+1)2≥36+![]() (x1x2+4)2,当x1x2=-4时,y有最小值,y+1≥3,y≥2, 即N点纵坐标最小值为2.
(x1x2+4)2,当x1x2=-4时,y有最小值,y+1≥3,y≥2, 即N点纵坐标最小值为2.
(1)∵抛物线有最低点,
∴a>0,
∵抛物线的顶点坐标为(h,k)在x轴正半轴上,
∴h>0,k=0;
(2)①∵当![]() 时,
时,![]() ;则
;则![]() ,
,
∴当x<0时,y随x的增大而减小,
当![]() 时,
时,![]() ;则
;则![]()
∴当x>0时,y随x的增大而增大,
∴抛物线的对称轴是![]() 轴,且开口向上
轴,且开口向上
又顶点在![]() 轴上,所以顶点是原点
轴上,所以顶点是原点![]()
∴抛物线的解析式为![]() ,且
,且![]()
当![]() 是等腰直角三角形,
是等腰直角三角形,![]() 时,
时,![]() ,
,
又![]() 为顶点,所以点
为顶点,所以点![]() 关于抛物线对称轴
关于抛物线对称轴![]() 轴对称.
轴对称.
![]() ,
,![]()
∴![]()
设![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() ,
,
∴点![]() 中一个坐标为
中一个坐标为![]() ,另一个为
,另一个为![]()
把![]() 代入
代入![]() ,解得
,解得![]()
∴抛物线的解析式为![]()
②PQ2=(x1-x2)2+(y1-y2)2≥36,
∵y1=![]() x12,y2=
x12,y2=![]() x22,
x22,
∴PQ2=(x1-x2)2+(y1-y2)2
=(x1-x2)2+(![]() x12-
x12-![]() x22)2
x22)2
=(x1-x2)2+![]() (x12+x22)2-
(x12+x22)2-![]() x12x22
x12x22
=x12+x22-2x1x2+![]() (x12+x22)2-
(x12+x22)2-![]() x12x22
x12x22
=4(y1+y2)+(y1+y2)2-![]() (x12x22+8x1x2)
(x12x22+8x1x2)
=4(y1+y2)+(y1+y2)2-![]() (x12x22+8x1x2+16-16)
(x12x22+8x1x2+16-16)
=4(y1+y2)+(y1+y2)2-![]() (x1x2+4)2+4
(x1x2+4)2+4
∵设N点坐标为(x,y),N是PQ的中点,
∴![]() >0
>0
∴2x=x1+x2,2y=y1+y2,
∴PQ2=8y+4y2-![]() (x1x2+4)2+4≥36,
(x1x2+4)2+4≥36,
∴4(y+1)2≥36+![]() (x1x2+4)2,
(x1x2+4)2,
∵y+1>0
当x1x2=-4时,y有最小值,
∴y+1≥3,
∴y≥2,
∴点N纵坐标的最小值为2


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】 爱好数学的甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字-1,0,1且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为p的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为q值,两次结果记为(p,q).
(1)请你帮他们用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D为顶点,连接BD,CD,抛物线的对称轴与x轴交与点E.
(1)求抛物线解析式及点D的坐标;
(2)G是抛物线上B,D之间的一点,且S四边形CDGB=4S△DGB,求出G点坐标;
(3)在抛物线上B,D之间是否存在一点M,过点M作MN⊥CD,交直线CD于点N,使以C,M,N为顶点的三角形与△BDE相似?若存在,求出满足条件的点M的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
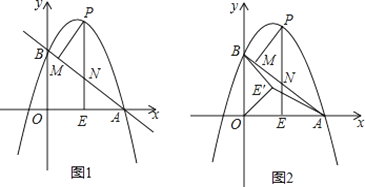
【题目】如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1,△AEN的周长为C2,若![]() ,求m的值;
,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接AE′、BE′,求AE′+![]() BE′的最小值.
BE′的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于 A,B 两点,与 x 轴相交于点 C.已知 tan∠BOC=
的图象相交于 A,B 两点,与 x 轴相交于点 C.已知 tan∠BOC=![]() ,点 B 的坐标为(m,n).
,点 B 的坐标为(m,n).
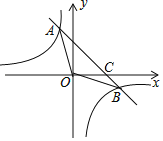
(1)求反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ECFD各顶点在Rt△ABC的边上,观察图形,并回答下列问题:
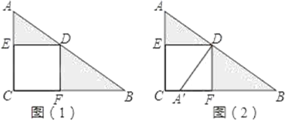
(1)请你说明由图(1)变换到图(2)的过程;
(2)若AD=3,△AED与△BDF的面积和为9,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
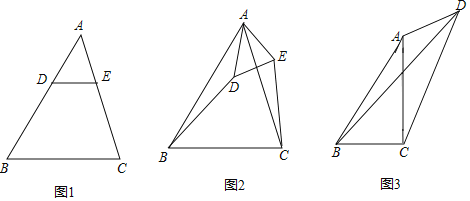
【题目】(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE=![]() ,则
,则![]() 的值是 ;
的值是 ;
(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD,![]() 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ=![]() ,当CD=6,AD=3时,请直接写出线段BD的长度.
,当CD=6,AD=3时,请直接写出线段BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,课题小组随机选取该校部分学生进行了问卷调査(问卷调査表如图1所示),并根据调查结果绘制了图2、图3两幅统计图(均不完整),请根据统计图解答下列问题.
(1)本次接受问卷调查的学生有________名.
(2)补全条形统计图.
(3)扇形统计图中B类节目对应扇形的圆心角的度数为________.
(4)该校共有2000名学生,根据调查结果估计该校最喜爱新闻节目的学生人数.

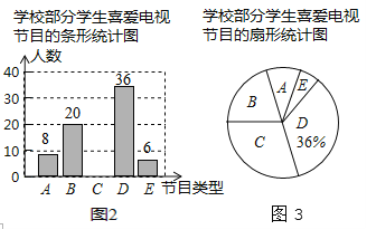
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com