
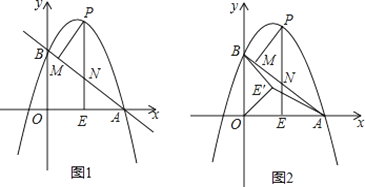
【题目】如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1,△AEN的周长为C2,若![]() ,求m的值;
,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接AE′、BE′,求AE′+![]() BE′的最小值.
BE′的最小值.
【答案】(1)a=-![]() ,y=-
,y=-![]() x+3;(2)2;(3)
x+3;(2)2;(3)![]() .
.
【解析】
令y=0,求出抛物线与x轴交点,列出方程即可求出a,根据待定系数法可以确定直线AB解析式.
由△PNM∽△ANE,推出![]() =
=![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
在y轴上,取一点M使得OM=![]() ,构造相似三角形,可以证明AM就是E′A+
,构造相似三角形,可以证明AM就是E′A+![]() E′B的最小值.
E′B的最小值.
将A(4,0)代入抛物线解析式得,a=-![]() ,抛物线解析式为
,抛物线解析式为![]() -
-![]()
当x=0时,y=3,所以B(0,3),设直线解析式为y=kx+b,将A,B点的坐标代入得![]()
解得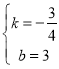
y=-![]()
(2)因为E(m,0)(0<m<4),
OE=m、AE=4-m、PE=-![]() m2+
m2+![]() m+3,①
m+3,①
由平行,可证 △AEN ∽△AOB,
因其对应边成比例,得
AN=![]() (4-m),NE=
(4-m),NE=![]() (4-m),
(4-m),
由两角相等,可证 △AEN∽△PMN,
又![]() =
=![]() ,得
,得
![]() =
=![]()
PN=![]() (4-m)
(4-m)
PE=PN+NE=![]() (4-m) ②,
(4-m) ②,
由①②得m=2或m=-4(负不合,舍)
所以m=2.
(3)由m=2得E(2,0),OE=OE′=2.
在y轴上取F,使![]() =
=![]() ,
,
(此处可得OF=![]() ,勾股定理得AF=
,勾股定理得AF=![]()
![]() )
)
又![]() =
=![]() ,
,
且∠FOE′=∠E′OB,
∴△FOE′∽△E′OB,
∴![]() =
=![]()
FE′=![]() E′B,
E′B,
E′A+![]() E′B=E′A+FE′≥AF=
E′B=E′A+FE′≥AF=![]()
![]()
最小值为![]()
![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 140元 B. 150元 C. 160元 D. 180元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
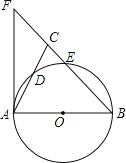
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点
的顶点![]() 在
在![]() 轴上.
轴上.
(1)若点![]() 是抛物线最低点,且落在
是抛物线最低点,且落在![]() 轴正半轴上,直接写出
轴正半轴上,直接写出![]() 的取值范围;
的取值范围;
(2)![]() ,
,![]() 是抛物线上两点,若
是抛物线上两点,若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,且当
,且当![]() 的绝对值为4时,
的绝对值为4时,![]() 为等腰直角三角形(其中
为等腰直角三角形(其中![]() ).
).
①求抛物线的解析式;
②设![]() 中点为
中点为![]() ,若
,若![]() ,求点
,求点![]() 纵坐标的最小值.
纵坐标的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)用画树状图法或列表法分析这两辆汽车行驶方向所有可能的结果;
(2)求一辆车向右转,一辆车向左转的概率;
(3)求至少有一辆车直行的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com