
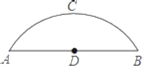
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
【答案】(1)r=6.5;(2)此货船能不顺利通过这座拱桥,见解析
【解析】
(1)根据垂径定理和勾股定理求解;
(2)连接ON,OB,通过求距离水面2米高处即ED长为2时,桥有多宽即MN的长与货船顶部的3米做比较来判定货船能否通过.先根据半弦,半径和弦心距构造直角三角形求出半径的长,再根据Rt△OEN中勾股定理求出EN的长,从而求得MN的长.
解:(1)如图,连接ON,OB.
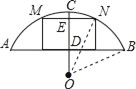
∵OC⊥AB,
∴D为AB中点,
∵AB=12m,
∴BD=![]() AB=6m.
AB=6m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+62,
解得:r=6.5.
(2)∵CD=4m,船舱顶部为长方形并高出水面AB=2m,
∴CE=4﹣3.6=0.4(m),
∴OE=r﹣CE=6.5﹣0.4=6.1(m),
在Rt△OEN中,EN2=ON2﹣OE2=6.52﹣6.12=5.04(m2),
∴EN=![]() (m).
(m).
∴MN=2EN=2×![]() ≈4.48m<5m.
≈4.48m<5m.
∴此货船能不顺利通过这座拱桥.


科目:初中数学 来源: 题型:
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
(1)点A的坐标:_____;点B的坐标:_____;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点D是直线AB上一动点(不包含点A,B),过点B作BE⊥CD于点E,连接EA.

(1)如图1,当点D在线段AB上时,直接写出线段CE,BE,AE的数量关系:______.
(2)如图2,当点D在线段AB的延长线上时,判断线段CE,BE,AE的数量关系,并加以证明.
(3)如图3,当点D在线段BA的延长线上时,并将已知条件中的“AB=AC”改成;![]() ,其他条件不变,若CE=1,
,其他条件不变,若CE=1,![]() ,请直接写出线段BE的长.
,请直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,∠ADB=∠CDB=∠BAC=45°,结论:①∠ABC=90°,②AB=BC,③AD2+DC2=2AB2,④AD+DC=![]() BD,其中正确的有( )
BD,其中正确的有( )
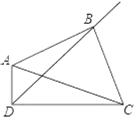
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
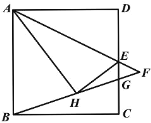
【题目】如图,在正方形ABCD中,AB=2,点E是CD的中点,连接AE,将△ADE沿AE折叠至△AHE,连接BH,延长AE,BH交于点F;BF,CD交于点G,则FG=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
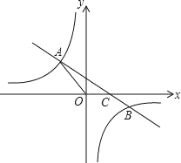
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使△APC是直角三角形?若存,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
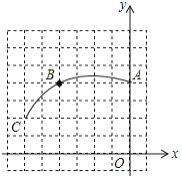
【题目】如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过格点![]() 、
、![]() 、
、![]() ,若该圆弧所在圆的圆心为
,若该圆弧所在圆的圆心为![]() 点,请你利用网格图回答下列问题:
点,请你利用网格图回答下列问题:
(1)圆心![]() 的坐标为_____;
的坐标为_____;
(2)若扇形![]() 是一个圆锥的侧面展开图,求该圆锥底面圆的半径长(结果保留根号).
是一个圆锥的侧面展开图,求该圆锥底面圆的半径长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
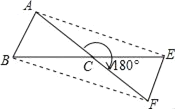
【题目】将△ABC绕点C旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由.
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com