
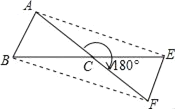
【题目】将△ABC绕点C旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由.
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
【答案】(1)AE∥BF,AE=BF,理由详见解析;(2)12cm2.
【解析】
(1)根据旋转的性质得![]() ,可得AB=FE,再根据∠ABC=∠FEC可得AB∥FE,即可证明四边形ABFE为平行四边形,从而得证AE∥BF,AE=BF.
,可得AB=FE,再根据∠ABC=∠FEC可得AB∥FE,即可证明四边形ABFE为平行四边形,从而得证AE∥BF,AE=BF.
(2)根据平行四边形的性质可得AC=CF,BC=CE,再根据等底同高可得四边形ABFE的面积.
解:(1)AE∥BF,AE=BF.
理由是:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴![]() ,
,
∴AB=FE,
∵∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形,
∴AE∥BF,AE=BF;
(2)由(1)得四边形ABFE为平行四边形,
∴AC=CF,BC=CE,
∴根据等底同高得到S△ABC=S△ACE=S△BCF=S△CEF=3cm2,
S四边形ABFE=4S△ABC=12cm2.


科目:初中数学 来源: 题型:
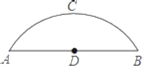
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市今年 1 月份的销售额为 500 万元,超市预计每个月的销售额会逐月增加.预测 3 月 份的销售额比 2 月份增加 120 万元;
(1)求 2、3 月份平均每月销售额的增长率;
(2)按照这样的增长速度,超市想在第一季度完成 1800 万元的销售目标是否能实现?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10,动点E、F分别在边AB、AD上,且AF=![]() AE.将△AEF绕点E顺时针旋转90°得到△A'EF',设AE=x,△A'EF'与矩形ABCD重叠部分面积为S,S的最大值为9.
AE.将△AEF绕点E顺时针旋转90°得到△A'EF',设AE=x,△A'EF'与矩形ABCD重叠部分面积为S,S的最大值为9.
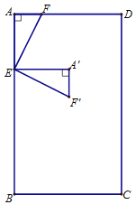
(1)求AD的长;
(2)求S关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
(1)求证:直线AB是⊙O的切线;
(2)OA,OB分别交⊙O于点D,E,AO的延长线交⊙O于点F,若AB=4AD,求sin∠CFE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市教育局组织部分教师分别到A、B、C、D四个地方进行课程培训,教育局按定额购买了前往四地的车票,如图1是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
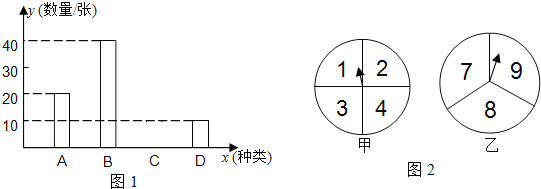
(1)若去A地的车票占全部车票的20%,求去C地的车票数,并补全条形统计图(图1);
(2)请从小到大写出这四类车票数的数字,并直接写出这四个数据的平均数和中位数;
(3)如图2,甲转盘被分成四等份且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,具体规定是:同时转动两个转盘,当指针指向的两个数字之和是偶数时,李老师出去培训,否则张老师出去培训(指针指在线上重转),试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.

(1)请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;
(2)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;
(3)开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( )
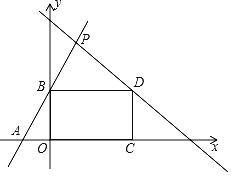
A.(2,8)B.![]() C.
C.![]() D.(4,12)
D.(4,12)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com