
【题目】如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
(1)求证:直线AB是⊙O的切线;
(2)OA,OB分别交⊙O于点D,E,AO的延长线交⊙O于点F,若AB=4AD,求sin∠CFE的值.

【答案】(1)见解析;(2)![]()
【解析】
(1)根据等腰三角形性质得出OC⊥AB,根据切线的判定得出即可;
(2)连接OC、DC,证△ADC∽△ACF,求出AF=4x,CF=2DC,根据勾股定理求出DC=![]() x,DF=3x,解直角三角形求出sin∠AFC,即可求出答案.
x,DF=3x,解直角三角形求出sin∠AFC,即可求出答案.
(1)证明:连接OC,如图1,
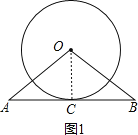
∵OA=OB,AC=BC,
∴OC⊥AB,
∵OC过O,
∴直线AB是⊙O的切线;
(2)解:连接OC、DC,如图2,
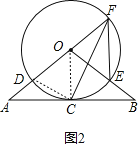
∵AB=4AD,
∴设AD=x,则AB=4x,AC=BC=2x,
∵DF为直径,
∴∠DCF=90°,
∵OC⊥AB,
∴∠ACO=∠DCF=90°,
∴∠OCF=∠ACD=90°﹣∠DCO,
∵OF=OC,
∴∠AFC=∠OCF,
∴∠ACD=∠AFC,
∵∠A=∠A,
∴△ADC∽△ACF,
∴![]() ,
,
∴AF=2AC=4x,FC=2DC,
∵AD=x,
∴DF=4x﹣x=3x,
在Rt△DCF中,(3x)2=DC2+(2DC)2,
解得:DC=![]() x,
x,
∵OA=OB,AC=BC,
∴∠AOC=∠BOC,
∴![]() ,
,
∴∠CFE=∠AFC,
∴sin∠CFE=sin∠AFC=![]() =
=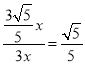 .
.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
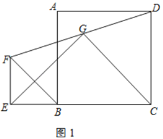
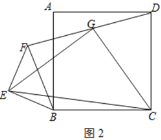
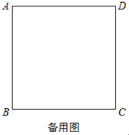
【题目】四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.
(1)问题发现:如图1,若点E在CB的延长线上,直接写出EG与GC的位置关系及![]() 的值;
的值;
(1)操作探究:将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(2)解决问题:将图1中的△BEF绕点B顺时针旋转,若BE=1,AB=![]() ,当E,F,D三点共线时,请直接写出CE的长.
,当E,F,D三点共线时,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
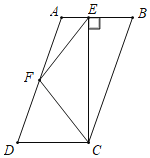
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是_____(把所有正确结论的序号部填在横线上).①∠AEF=![]() ∠DFE;②S△BEC=2S△CEF;③EF=CF;④∠BCD=2∠DCF.
∠DFE;②S△BEC=2S△CEF;③EF=CF;④∠BCD=2∠DCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新区一中为了了解同学们课外阅读的情况,现对初三某班进行了“你最喜欢的课外书籍类别”的问卷调查.用“![]() "表示小说类书籍,“
"表示小说类书籍,“![]() ”表示文学类书籍,“
”表示文学类书籍,“![]() ”表示传记类书籍,“
”表示传记类书籍,“![]() ”表示艺术类书籍.根据问卷调查统计资料绘制了如下两副
”表示艺术类书籍.根据问卷调查统计资料绘制了如下两副
不完整的统计图.
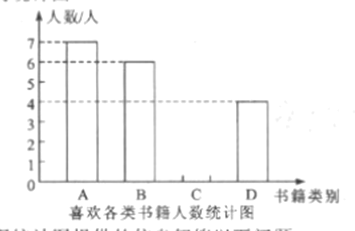
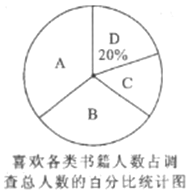
请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了 名学生,请补全条形统计图;
(2)在接受问卷调查的学生中,喜欢“![]() ”的人中有2名是女生,喜欢“
”的人中有2名是女生,喜欢“![]() ”的人中有2名是女生,现分别从喜欢这两类书籍的学生中各选1名进行读书心得交流,请用画树状图或列表法求出刚好选中2名是一男一女的概率.
”的人中有2名是女生,现分别从喜欢这两类书籍的学生中各选1名进行读书心得交流,请用画树状图或列表法求出刚好选中2名是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
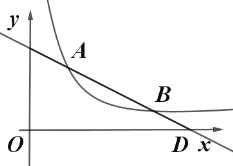
(1)求直线和反比例函数的解析式;
(2)若直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,嘉淇认为
,嘉淇认为![]() ,请通过计算说明她的观点是否正确.
,请通过计算说明她的观点是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点P为抛物线上一点(不与点A重合),连接PC.当∠PCB=∠ACB时,求点P的坐标;
(3)在(2)的条件下,将抛物线沿平行于y轴的方向向下平移,平移后的抛物线的顶点为点D,点P的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.
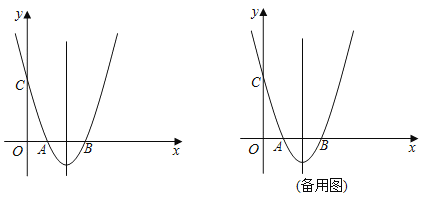
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com