
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
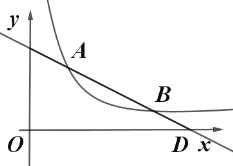
(1)求直线和反比例函数的解析式;
(2)若直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,嘉淇认为
,嘉淇认为![]() ,请通过计算说明她的观点是否正确.
,请通过计算说明她的观点是否正确.
【答案】(1)直线的解析式为![]() ;反比例函数的解析式为
;反比例函数的解析式为![]() .(2)嘉淇的观点正确.理由见解析
.(2)嘉淇的观点正确.理由见解析
【解析】
(1)分别把![]() 代入直线
代入直线![]() 和反比例函数
和反比例函数![]() ,求出a,k的值,即可求出直线和反比例函数的解析式;
,求出a,k的值,即可求出直线和反比例函数的解析式;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,联立
,联立![]() 和
和![]() ,解方程组求出x的值,即可求出
,解方程组求出x的值,即可求出![]() ,
,![]() ,由直线解析式可求出C、D点的坐标,从而求出OC,OD的 长,根据
,由直线解析式可求出C、D点的坐标,从而求出OC,OD的 长,根据![]() ,即可推出结论.
,即可推出结论.
(1)∵直线![]() 过点
过点![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴直线的解析式为![]() ;
;
∵反比例函数![]() 的图象过点
的图象过点![]() ,
,
∴![]() ,
,
∴反比例函数的解析式为![]() .
.
(2)如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,
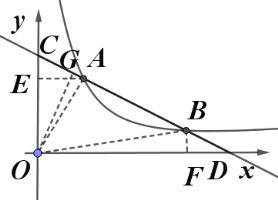
联立![]() 和
和![]() ,整理得
,整理得![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∴嘉淇的观点正确.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )

A.106cmB.110cmC.114cmD.116cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
(1)求证:直线AB是⊙O的切线;
(2)OA,OB分别交⊙O于点D,E,AO的延长线交⊙O于点F,若AB=4AD,求sin∠CFE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
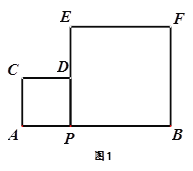
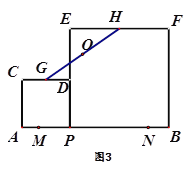
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC与正方形PBFE.
(1)在点P运动时,这两个正方形面积之和是定值吗?如果时求出;若不是,求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点A,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
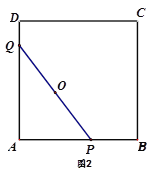
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向D点运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图(3),在“问题思考”中,若点M、N是线段AB上的两点,且AM=BM=1,点G、H分别是边CD、EF的中点.请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点.动点
中点.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,点
运动,点![]() 关于点
关于点![]() 对称点为点
对称点为点![]() ,以
,以![]() 为边向上作正方形
为边向上作正方形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
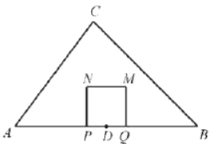
(1)当![]() _______秒时,点
_______秒时,点![]() 落在
落在![]() 边上.
边上.
(2)设正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() ,当点
,当点![]() 在
在![]() 内部时,求
内部时,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)当正方形![]() 的对角线所在直线将
的对角线所在直线将![]() 的分为面积相等的两部分时,直接写出
的分为面积相等的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
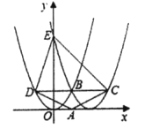
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 的图像交于点
的图像交于点![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交两抛物线于
轴的平行线交两抛物线于![]() 、
、![]() 两点.若点
两点.若点![]() 是
是![]() 轴上两抛物线顶点之间的一点,连结
轴上两抛物线顶点之间的一点,连结![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为________(用含
的面积为________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
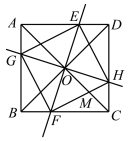
【题目】如图,已知正方形ABCD,O为对角线AC与BD的交点,过点O的直线EF与直线GH分别交AD,BC,AB,CD于点E,F,G,H,若EF⊥GH,OC与FH相交于点M,当CF=4,AG=2时,则OM的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从A地出发以每小时80km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶3小时后,在距B地160km处与轿车相遇.图中线段表示货车离B地的距离y1与货车行驶的时间x的关系.
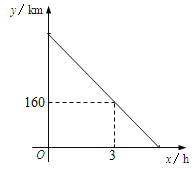
(1)AB两地之间的距离为 km;
(2)求y1与x之间的函数关系式;
(3)若两车同时到达各自目的地,在同一坐标系中画出轿车离B地的距离y2与货车行驶时间x的函数图像,用文字说明该图像与x轴交点所表示的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
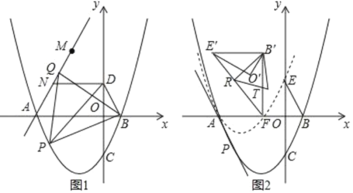
【题目】如图,在平面直角标系中,抛物线C:y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=![]() OC,连接BD,
OC,连接BD,
(1)如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+![]() AM的最小值
AM的最小值
(2)如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y=![]() 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com