
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点.动点
中点.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,点
运动,点![]() 关于点
关于点![]() 对称点为点
对称点为点![]() ,以
,以![]() 为边向上作正方形
为边向上作正方形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
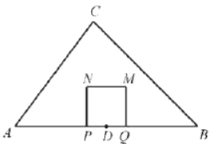
(1)当![]() _______秒时,点
_______秒时,点![]() 落在
落在![]() 边上.
边上.
(2)设正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() ,当点
,当点![]() 在
在![]() 内部时,求
内部时,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)当正方形![]() 的对角线所在直线将
的对角线所在直线将![]() 的分为面积相等的两部分时,直接写出
的分为面积相等的两部分时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)如下图,根据![]() ,可得出PN与AP的关系,从而求出t的值;
,可得出PN与AP的关系,从而求出t的值;
(2)如下图,存在2种情况,一种是点M在△ABC内,另一种是点M在△ABC外部,分别根据正方形和三角形求面积的公式可求解;
(3)如下图,存在2种情况,一种是PM所在的直线将△ABC的面积平分,另一种是QN所在的直线将△ABC的面积平分.
(1)如图1,点N在AC上
图1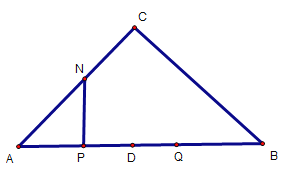
由题意可知:PD=DQ=t,AP=7-t
∴PN=PQ=2t
∵![]()
∴![]() ,即
,即![]()
解得:t=![]()
(2)①如图2,
图2
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,即
,即![]()
解得![]() ,
,
故当![]() ≤
≤![]() 时,
时,![]() ;
;
②如图3,
图3
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
则![]()
![]() ;
;
综上, .
.
(3)如下图,过点C作AB的垂线,交AB于点G
图4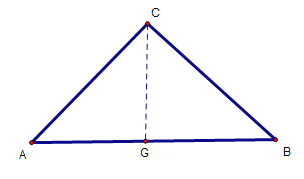
∵![]()
∴设CG=4x,则AG=3x
∵∠B=45°
∴△CBG是等腰直角三角形
∴GB=GC=4x
∵AB=14
∴3x+4x=14,解得:x=2
∴![]()
∴![]()
情况一:PM所在的直线平分△ABC的面积,如下图,PM与BC交于点E
图5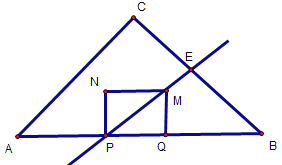
则![]()
∵四边形PQMN是正方形,∴∠EPB=45°
∵∠B=45°
∴△PBE是等腰直角三角形
∵![]()
∴PE=PB=![]()
∴PB=![]()
∵PB=AB-PA=14-(7-t)=7+t
∴7+t=![]()
t=![]()
情况二:如下图,QN所在线段平分△ABC的面积,QF交AC于点F,过点F作AB的垂线,交AB于点H
图6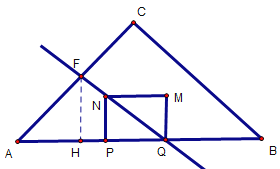
同理,![]()
∵四边形PQMN是正方形,∴∠EQH=45°
∴△FHQ是等腰直角三角形
∵![]()
∴设FH=4y,则AH=3y,HQ=FH=4y,∴AQ=7y
∴![]() ,解得:y=
,解得:y=![]()
∵AQ=AB-QB=14-(7-t)=7+t
∴7+t=7![]()
解得:t=7![]()
∴综上得:![]() 的值为
的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
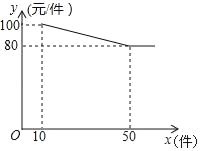
【题目】服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x为正整数)之间所满足的函数关系如图所示.
(1)求y与x之间所满足的函数关系式,并写出x的取值范围;
(2)设服装厂所获利润为w(元),若10≤x≤50(x为正整数),求批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
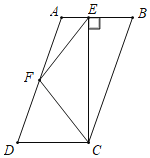
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是_____(把所有正确结论的序号部填在横线上).①∠AEF=![]() ∠DFE;②S△BEC=2S△CEF;③EF=CF;④∠BCD=2∠DCF.
∠DFE;②S△BEC=2S△CEF;③EF=CF;④∠BCD=2∠DCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
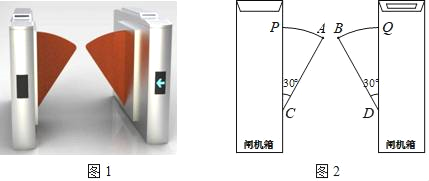
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
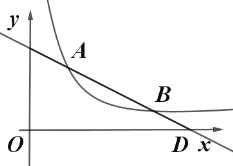
(1)求直线和反比例函数的解析式;
(2)若直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,嘉淇认为
,嘉淇认为![]() ,请通过计算说明她的观点是否正确.
,请通过计算说明她的观点是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家自2016年1月1日起实行全面放开二胎政策,某计生组织为了解该市家庭对待这项政策的态度,准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取1 000户家庭调查;
B.从一个城镇的不同住宅楼中随机选取1 000户家庭调查;
C.从该市公安局户籍管理处随机抽取1 000户城乡家庭调查.
(1)在上述调查方式中,你认为比较合理的一个是【1】.(填“A”、“B”或“C”)
(2)将一种比较合理的调查方式调查得到的结果分为四类:(A)已有两个孩子;
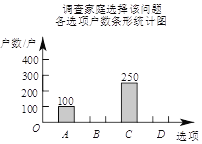
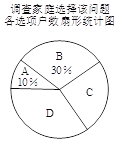
(B)决定生二胎;(C)考虑之中;(D)决定不生二胎.将调查结果绘制成如下两幅不完整的统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
①补全条形统计图.
②估计该市100万户家庭中决定不生二胎的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为等边
为等边![]() 的高,
的高,![]() ,点P为直线
,点P为直线![]() 上的动点(不与点B重合),连接
上的动点(不与点B重合),连接![]() ,将线段
,将线段![]() 绕点P逆时针旋转60°,得到线段
绕点P逆时针旋转60°,得到线段![]() ,连接
,连接![]() 、
、![]() .
.
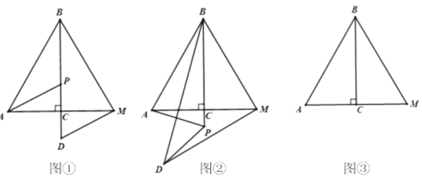
(1)问题发现:如图①,当点D在直线![]() 上时,线段
上时,线段![]() 与
与![]() 的数量关系为_________,
的数量关系为_________,![]() _________;
_________;
(2)拓展探究:如图②,当点P在![]() 的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)问题解决:当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③△POF∽△BNF;④当△PMN∽△AMP时,点P是AB的中点,其中一定正确的结论有_____.(填上所有正确的序号).
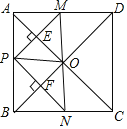
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com