
【题目】一辆货车从A地出发以每小时80km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶3小时后,在距B地160km处与轿车相遇.图中线段表示货车离B地的距离y1与货车行驶的时间x的关系.
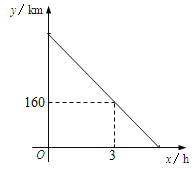
(1)AB两地之间的距离为 km;
(2)求y1与x之间的函数关系式;
(3)若两车同时到达各自目的地,在同一坐标系中画出轿车离B地的距离y2与货车行驶时间x的函数图像,用文字说明该图像与x轴交点所表示的实际意义.
【答案】(1)400;(2)y1=-80x+400;(3)详见解析,货车从A地出发![]() 小时后,轿车从B地出发.
小时后,轿车从B地出发.
【解析】
(1)根据货车行驶的路程+货车离B地的路程即可得出A、B两地之间的距离;
(2)根据函数图象经过的点设出一次函数的解析式用待定系数法求一次函数的解析式即可;
(3)作出一次函数的图象并根据图象得到交点坐标所表示的意义是货车从A地出发![]() 小时后轿车从B地出发.
小时后轿车从B地出发.
(1)AB两地之间的距离为:80×3+160=400km,
故答案为:400;
(2)因为货车从A地出发以每小时80km的速度匀速驶往B地,
所以y1+80x=b,代入点(3,160),得b=400.
∴y1=-80x+400;
(3)如图,线段y2即为所求的图像;
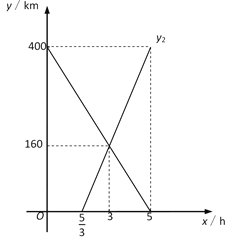
货车行驶的时间为400÷80=5h,则可求设y2的函数表达式为y2=mx+n
把(5,400),(3,160)分别代入y2=mx+n得,
![]()
解得,![]()
∴y2=120x-200,
当y=0时,x=![]() ,
,
故该图像与x轴交点坐标为(![]() ,0).
,0).
它表示的实际意义:货车从A地出发![]() 小时后,轿车从B地出发.
小时后,轿车从B地出发.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
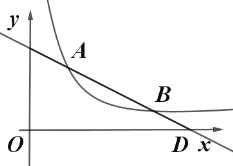
(1)求直线和反比例函数的解析式;
(2)若直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,嘉淇认为
,嘉淇认为![]() ,请通过计算说明她的观点是否正确.
,请通过计算说明她的观点是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,点A(
为原点,点A(![]() ,0),点B(0,1),点E是边AB中点,把
,0),点B(0,1),点E是边AB中点,把![]() 绕点A顺时针旋转,得△ADC,点O,B旋转后的对应点分别为D,C.记旋转角为
绕点A顺时针旋转,得△ADC,点O,B旋转后的对应点分别为D,C.记旋转角为![]() .
.
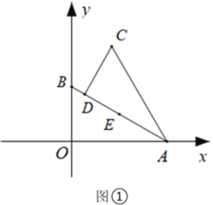
(Ⅰ)如图①,当点D恰好在AB上时,求点D的坐标;
(Ⅱ)如图②,若![]() 时,求证:四边形OECD是平行四边形;
时,求证:四边形OECD是平行四边形;
(Ⅲ)连接OC,在旋转的过程中,求△OEC面积的最大值(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为等边
为等边![]() 的高,
的高,![]() ,点P为直线
,点P为直线![]() 上的动点(不与点B重合),连接
上的动点(不与点B重合),连接![]() ,将线段
,将线段![]() 绕点P逆时针旋转60°,得到线段
绕点P逆时针旋转60°,得到线段![]() ,连接
,连接![]() 、
、![]() .
.
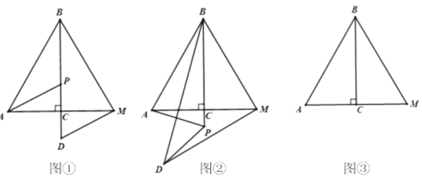
(1)问题发现:如图①,当点D在直线![]() 上时,线段
上时,线段![]() 与
与![]() 的数量关系为_________,
的数量关系为_________,![]() _________;
_________;
(2)拓展探究:如图②,当点P在![]() 的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)问题解决:当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念认识)
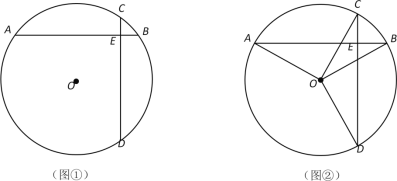
在同一个圆中两条互相垂直且相等的弦定义为“等垂弦”,两条弦所在直线的交点为等垂弦的分割点.如图①,AB、CD是⊙O的弦,AB=CD,AB⊥CD,垂足为E,则AB、CD是等垂弦,E为等垂弦AB、CD的分割点.
(数学理解)
(1)如图②,AB是⊙O的弦,作OC⊥OA、OD⊥OB,分别交⊙O于点C、D,连接CD.求证: AB、CD是⊙O的等垂弦.
(2)在⊙O中,⊙O的半径为5,E为等垂弦AB、CD的分割点,![]() .求AB的长度.
.求AB的长度.
(问题解决)
(3)AB、CD是⊙O的两条弦,CD=![]() AB,且CD⊥AB,垂足为F.
AB,且CD⊥AB,垂足为F.
①在图③中,利用直尺和圆规作弦CD(保留作图痕迹,不写作法).
②若⊙O的半径为r,AB=mr(m为常数),垂足F与⊙O的位置关系随m的值变化而变化,直接写出点F与⊙O的位置关系及对应的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
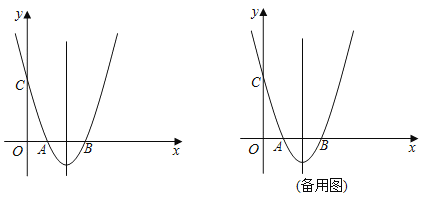
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点P为抛物线上一点(不与点A重合),连接PC.当∠PCB=∠ACB时,求点P的坐标;
(3)在(2)的条件下,将抛物线沿平行于y轴的方向向下平移,平移后的抛物线的顶点为点D,点P的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:以下是我们教科书中的一段内容,请仔细阅读,并解答有关问题.
公元前3世纪,古希腊学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡,后来人们把它归纳为“杠杆原理”,通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂

(问题解决)
若工人师傅欲用撬棍动一块大石头,已知阻力和阻力臂不变,分别为1500N和0.4m.
(1)动力F(N)与动力臂l(m)有怎样的函数关系?当动力臂为1.5m时,撬动石头需要多大的力?
(2)若想使动力F(N)不超过题(1)中所用力的一半,则动力臂至少要加长多少?
(数学思考)
(3)请用数学知识解释:我们使用棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com