
【题目】在平面直角坐标系中,![]() 为原点,点A(
为原点,点A(![]() ,0),点B(0,1),点E是边AB中点,把
,0),点B(0,1),点E是边AB中点,把![]() 绕点A顺时针旋转,得△ADC,点O,B旋转后的对应点分别为D,C.记旋转角为
绕点A顺时针旋转,得△ADC,点O,B旋转后的对应点分别为D,C.记旋转角为![]() .
.
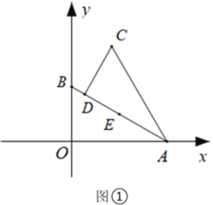
(Ⅰ)如图①,当点D恰好在AB上时,求点D的坐标;
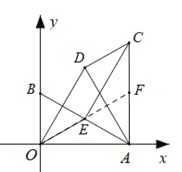
(Ⅱ)如图②,若![]() 时,求证:四边形OECD是平行四边形;
时,求证:四边形OECD是平行四边形;
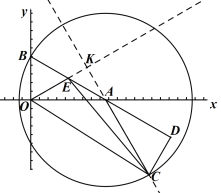
(Ⅲ)连接OC,在旋转的过程中,求△OEC面积的最大值(直接写出结果即可).

【答案】(Ⅰ)D(![]() -
-![]() ,
,![]() );(Ⅱ)证明见解析;(Ⅲ)
);(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
(1)先求出∠BAO的度数,然后求出AM、DM的长度,进而求出OM的长度,从而得出点D的坐标;
(2)先得出△BOE是等边三角形,得到OB=OE=DC,再得到OE∥DC,从而得出结论;
(3)以![]() 为圆心,
为圆心,![]() 为半径画
为半径画![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,当
,当![]() 三点共线时,此时高
三点共线时,此时高![]() 最大,面积最大,求出
最大,面积最大,求出![]() 的值,利用面积公式直接求解即可.
的值,利用面积公式直接求解即可.
解:(Ⅰ)由题意:OA=![]() ,OB=1,
,OB=1,
∴在△AOB中,∠AOB=90°,tan∠BAO=![]() ,
,
∴∠BAO=30°.
由旋转性质得,DA=OA=![]() ,
,
过D作DM⊥OA于M,
则在Rt△DAM中,DM=![]() ,AM=
,AM=![]() ,
,
∴OM=AO-OM=![]() -
-![]() ,
,
∴D(![]() -
-![]() ,
,![]() ).
).
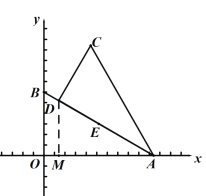
(Ⅱ)延长OE交AC于F,
在Rt△AOB 中,点E为AB的中点,∠BAO=30°,
∴OE=BE=AE.
又∠ABO=60°,∴△BOE是等边三角形,
∴OE=OB,∴∠BOE=60°,∴∠EOA=30°,
由旋转性质,DC=OB ,
∴OE=DC.
∵![]() ,
,
∴∠OAD=60°,
由旋转性质知,
∠DAC=∠OAB=30°,∠DCA=∠OBA=60°,
∴∠OAC=∠OAD+∠DAC=90°,
∴∠OFA=90°-∠EOA=90°-30°=60°,
∴∠DCA=∠OFA,
∴OE∥DC.
∴四边形OECD是平行四边形.
(III)以![]() 为圆心,
为圆心,![]() 为半径画
为半径画![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
在![]() ,
,
∵∠BAO=30°,
∴![]() ,
,
∵![]() 为
为![]() 中点,
中点,![]() 是直角三角形,
是直角三角形,
∴![]() ,
,
∴![]() ,
,
∵圆中最长的弦是直径,
∴当点![]() 旋转到如图所示的位置时,即
旋转到如图所示的位置时,即![]() 三点共线时,此时高
三点共线时,此时高![]() 最大,面积最大,
最大,面积最大,
∵![]() ,
,
∴在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
此时,![]() ;
;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
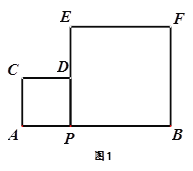
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC与正方形PBFE.
(1)在点P运动时,这两个正方形面积之和是定值吗?如果时求出;若不是,求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点A,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
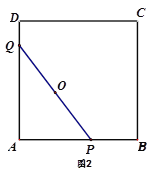
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向D点运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
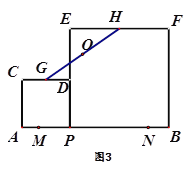
(4)如图(3),在“问题思考”中,若点M、N是线段AB上的两点,且AM=BM=1,点G、H分别是边CD、EF的中点.请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
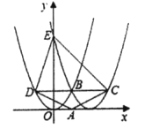
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 的图像交于点
的图像交于点![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交两抛物线于
轴的平行线交两抛物线于![]() 、
、![]() 两点.若点
两点.若点![]() 是
是![]() 轴上两抛物线顶点之间的一点,连结
轴上两抛物线顶点之间的一点,连结![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为________(用含
的面积为________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
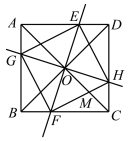
【题目】如图,已知正方形ABCD,O为对角线AC与BD的交点,过点O的直线EF与直线GH分别交AD,BC,AB,CD于点E,F,G,H,若EF⊥GH,OC与FH相交于点M,当CF=4,AG=2时,则OM的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式变得更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息回答下列问题:

(1)本次调查共调查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为______;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从A地出发以每小时80km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶3小时后,在距B地160km处与轿车相遇.图中线段表示货车离B地的距离y1与货车行驶的时间x的关系.
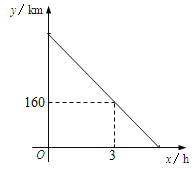
(1)AB两地之间的距离为 km;
(2)求y1与x之间的函数关系式;
(3)若两车同时到达各自目的地,在同一坐标系中画出轿车离B地的距离y2与货车行驶时间x的函数图像,用文字说明该图像与x轴交点所表示的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,求函数图像的顶点坐标(用含
时,求函数图像的顶点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)当y最大值为1时,且![]() ,求整数
,求整数![]() 的值;
的值;
(3)当直线![]() 与函数
与函数![]() 的图像只有一个公共点时,求
的图像只有一个公共点时,求![]() 的取值范围;
的取值范围;
(4)设点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上的正半轴上,已知点
轴上的正半轴上,已知点![]() ,以
,以![]() 为边做正方形
为边做正方形![]() ,当函数
,当函数![]() 的图像与正方形
的图像与正方形![]() 的边有两个公共点时,直接写出
的边有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
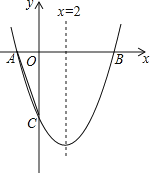
【题目】如图,在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 图象经过点
图象经过点![]() ,
,![]() ,其对称轴为直线
,其对称轴为直线![]() .
.
(1)求该二次函数的解析式;
(2)若直线![]() 将
将![]() 的面积分成相等的两部分,求
的面积分成相等的两部分,求![]() 的值;
的值;
(3)点![]() 是该二次函数图象与
是该二次函数图象与![]() 轴的另一个交点,点
轴的另一个交点,点![]() 是直线
是直线![]() 上位于
上位于![]() 轴下方的动点,点
轴下方的动点,点![]() 是第四象限内该二次函数图象上的动点,且位于直线
是第四象限内该二次函数图象上的动点,且位于直线![]() 右侧.若以点
右侧.若以点![]() 为直角顶点的
为直角顶点的![]() 与
与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com