
【题目】在平面直角坐标系中,已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,求函数图像的顶点坐标(用含
时,求函数图像的顶点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)当y最大值为1时,且![]() ,求整数
,求整数![]() 的值;
的值;
(3)当直线![]() 与函数
与函数![]() 的图像只有一个公共点时,求
的图像只有一个公共点时,求![]() 的取值范围;
的取值范围;
(4)设点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上的正半轴上,已知点
轴上的正半轴上,已知点![]() ,以
,以![]() 为边做正方形
为边做正方形![]() ,当函数
,当函数![]() 的图像与正方形
的图像与正方形![]() 的边有两个公共点时,直接写出
的边有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() ;(4)
;(4)![]() 或
或![]() 或
或![]()
【解析】
(1)把函数![]() 配方成顶点式即可求得;
配方成顶点式即可求得;
(2)分两类情况:当![]() 时,
时, ![]() ,当
,当![]() 时,
时,![]() ,结合
,结合![]() ,即可算出n的值;
,即可算出n的值;
(3)分两类情况:当![]() 时,交点即是抛物线的顶点,当
时,交点即是抛物线的顶点,当![]() 时,满足
时,满足![]() 即可;
即可;
(4)数形结合的方法,看两个交点在哪些边上,分类讨论,结合点的坐标即可算出n的取值范围.
(1)![]()
所以当![]() 时,顶点坐标为
时,顶点坐标为![]()
(2) 当![]() 时,
时, ![]() ;
;
当![]() 时,
时,![]()
![]() 且是整数
且是整数
所以![]() 或
或![]() 或
或![]()
(3)当![]() 时, 交点即是抛物线的顶点,
时, 交点即是抛物线的顶点,![]() ,如图①
,如图①
解得:![]() (舍去),
(舍去),![]()
当![]() 时,满足
时,满足![]() 即可,解得
即可,解得![]() 如图②
如图②
综上得,n的取值范围是![]() 或
或![]()
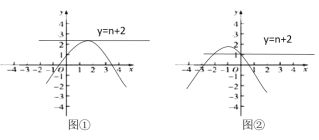
(4)
当两个交点都在AC上时,如图③,则经过C点(2n,2n),得:![]() ;
;
当一个交点在OA上,一个交点在BC上时,如图④,则顶点在AC之下,即:![]() ;
;
当交点在OB和BC上时,则![]() ,且抛物线在B点下方,如图⑥即:
,且抛物线在B点下方,如图⑥即:![]() 或
或![]() (舍去),
(舍去),
综上可得,n的取值范围是:![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】新区一中为了了解同学们课外阅读的情况,现对初三某班进行了“你最喜欢的课外书籍类别”的问卷调查.用“![]() "表示小说类书籍,“
"表示小说类书籍,“![]() ”表示文学类书籍,“
”表示文学类书籍,“![]() ”表示传记类书籍,“
”表示传记类书籍,“![]() ”表示艺术类书籍.根据问卷调查统计资料绘制了如下两副
”表示艺术类书籍.根据问卷调查统计资料绘制了如下两副
不完整的统计图.
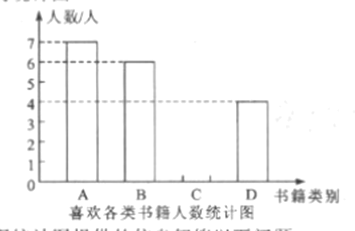
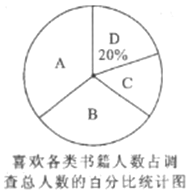
请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了 名学生,请补全条形统计图;
(2)在接受问卷调查的学生中,喜欢“![]() ”的人中有2名是女生,喜欢“
”的人中有2名是女生,喜欢“![]() ”的人中有2名是女生,现分别从喜欢这两类书籍的学生中各选1名进行读书心得交流,请用画树状图或列表法求出刚好选中2名是一男一女的概率.
”的人中有2名是女生,现分别从喜欢这两类书籍的学生中各选1名进行读书心得交流,请用画树状图或列表法求出刚好选中2名是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,点A(
为原点,点A(![]() ,0),点B(0,1),点E是边AB中点,把
,0),点B(0,1),点E是边AB中点,把![]() 绕点A顺时针旋转,得△ADC,点O,B旋转后的对应点分别为D,C.记旋转角为
绕点A顺时针旋转,得△ADC,点O,B旋转后的对应点分别为D,C.记旋转角为![]() .
.
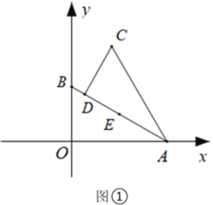
(Ⅰ)如图①,当点D恰好在AB上时,求点D的坐标;
(Ⅱ)如图②,若![]() 时,求证:四边形OECD是平行四边形;
时,求证:四边形OECD是平行四边形;
(Ⅲ)连接OC,在旋转的过程中,求△OEC面积的最大值(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念认识)
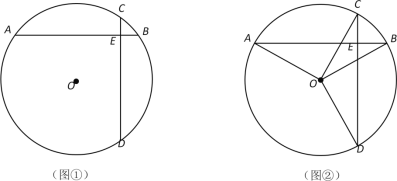
在同一个圆中两条互相垂直且相等的弦定义为“等垂弦”,两条弦所在直线的交点为等垂弦的分割点.如图①,AB、CD是⊙O的弦,AB=CD,AB⊥CD,垂足为E,则AB、CD是等垂弦,E为等垂弦AB、CD的分割点.
(数学理解)
(1)如图②,AB是⊙O的弦,作OC⊥OA、OD⊥OB,分别交⊙O于点C、D,连接CD.求证: AB、CD是⊙O的等垂弦.
(2)在⊙O中,⊙O的半径为5,E为等垂弦AB、CD的分割点,![]() .求AB的长度.
.求AB的长度.
(问题解决)
(3)AB、CD是⊙O的两条弦,CD=![]() AB,且CD⊥AB,垂足为F.
AB,且CD⊥AB,垂足为F.
①在图③中,利用直尺和圆规作弦CD(保留作图痕迹,不写作法).
②若⊙O的半径为r,AB=mr(m为常数),垂足F与⊙O的位置关系随m的值变化而变化,直接写出点F与⊙O的位置关系及对应的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
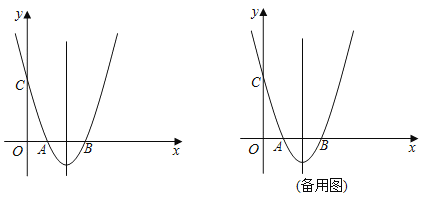
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点P为抛物线上一点(不与点A重合),连接PC.当∠PCB=∠ACB时,求点P的坐标;
(3)在(2)的条件下,将抛物线沿平行于y轴的方向向下平移,平移后的抛物线的顶点为点D,点P的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童用药的剂量常常按他们的体重来计算,某种药品,体重![]() 的儿童,每次正常服用量为
的儿童,每次正常服用量为![]() ;体重
;体重![]() 的儿童每次正常服用量为
的儿童每次正常服用量为![]() ;体重在
;体重在![]() 范围内时,每次正常服用量
范围内时,每次正常服用量![]() 是儿童体重
是儿童体重![]() 的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.
的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若该药品的一种包装规格为![]() /袋,求体重在什么范围的儿童生病时可以一次服下一袋药?
/袋,求体重在什么范围的儿童生病时可以一次服下一袋药?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水果按照果径大小可分为4个等级:标准果、优质果、精品果、礼品果,某采购商从采购的一批该种水果中随机抽取100个,利用它的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,售价为20元/个;
方案2:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/个) | 16 | 18 | 22 | 24 |
(1)从采购商的角度考虑,应该采用哪种购销方案?
(2)若采购商采购的该种水果的进价不超过20元/个,则采购商可以获利,现从这种水果的4个等级中任选2种,按方案2进行购买,求这2种等级的水果至少有一种能使采购商获利的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
(1)求证:CD为⊙O的切线.
(2)若![]() ,求cos∠DAB.
,求cos∠DAB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com