
科目: 来源: 题型:
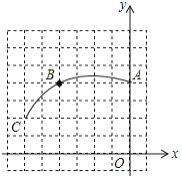
【题目】如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过格点![]() 、
、![]() 、
、![]() ,若该圆弧所在圆的圆心为
,若该圆弧所在圆的圆心为![]() 点,请你利用网格图回答下列问题:
点,请你利用网格图回答下列问题:
(1)圆心![]() 的坐标为_____;
的坐标为_____;
(2)若扇形![]() 是一个圆锥的侧面展开图,求该圆锥底面圆的半径长(结果保留根号).
是一个圆锥的侧面展开图,求该圆锥底面圆的半径长(结果保留根号).
查看答案和解析>>
科目: 来源: 题型:
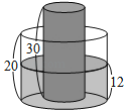
【题目】如图,有一内部装有水的直圆柱形水桶,桶高![]() ;另有一直圆柱形的实心铁柱,柱高
;另有一直圆柱形的实心铁柱,柱高![]() ,直立放置于水桶底面上,水桶内的水面高度为
,直立放置于水桶底面上,水桶内的水面高度为![]() ,且水桶与铁柱的底面半径比为
,且水桶与铁柱的底面半径比为![]() .今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为( )
.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
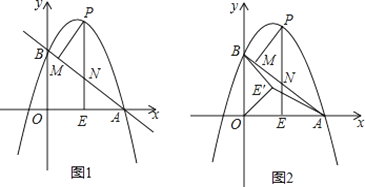
【题目】如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1,△AEN的周长为C2,若![]() ,求m的值;
,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接AE′、BE′,求AE′+![]() BE′的最小值.
BE′的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,边
,边![]() 的长为
的长为![]() 边
边![]() 的长为
的长为![]() ,在此三角形内有一个矩形
,在此三角形内有一个矩形![]() ;点
;点![]() 分别在
分别在![]() 上,设
上,设![]() 的长为
的长为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() (单位:
(单位: ![]() )
)
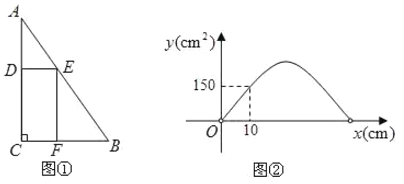
(1)当![]() 等于30时,求
等于30时,求![]() 与
与![]() 的函数关系式:(不要求写出自变量
的函数关系式:(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)在(1)的条件下,矩形![]() 的面积能否为
的面积能否为![]() ?请说明理由?
?请说明理由?
(3)若![]() 与
与![]() 的函数图象如图2所示,求此时
的函数图象如图2所示,求此时![]() 的值
的值
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司营销![]() 两种产品,根据市场调研,确定两条信息:
两种产品,根据市场调研,确定两条信息:
信息1:销售![]() 种产品所获利润
种产品所获利润![]() (万元)与所销售产品
(万元)与所销售产品![]() (吨)之间存在二次函数关系,如图所示
(吨)之间存在二次函数关系,如图所示
信息2:销售![]() 种产品所获利润
种产品所获利润![]() (万元)与销售产品
(万元)与销售产品![]() (吨)之间存在正比例函数关系
(吨)之间存在正比例函数关系![]()
根据以上信息,解答下列问题:

(1)求二次函数的表达式;
(2)该公司准备购进![]() 两种产品共10吨,请设计一个营销方案使销售
两种产品共10吨,请设计一个营销方案使销售![]() 两种产品获得的利润之和最大,最大利润是多少万元?
两种产品获得的利润之和最大,最大利润是多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60![]() 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120![]() 海里。
海里。

(1)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.45)
=2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com