如图，图形旋转多少度后能与自身重合

1. A.
   45°
2. B.
   60°
3. C.
   72°
4. D.
   90°

如图．边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转45°，则这两个正方形重叠部分的面积是

1. A.
   
2. B.
   
3. C.
   
4. D.
   

计算：=

1. A.
   
2. B.
   
3. C.
   
4. D.
   

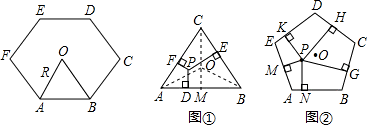同学们已经认识了很多正多边形，现以正六边形为例再介绍与正多边形相关的几个概念．如正六边形ABCDEF各边对称轴的交点O，又称正六边形的中心，其中OA称正六边形的半径，通常用R表示，∠AOB称为中心角，显然．提出问题：正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系？
探索发现：
（1）为了解决这个问题，我们不妨从最简单的正多边形--正三角形入手．
如图①，△ABC是正三角形，半径OA=R，∠AOB是中心角，P是△ABC内任意一点，P到△ABC各边距离分别为h₁、h₂、h₃ ，确定h₁+h₂+h₃的值与△ABC的半径R及中心角的关系．
解：设△ABC的边长是a，面积为S，显然S=a（h₁+h₂+h₃）
O为△ABC的中心，连接OA、OB、OC，它们将△ABC分成三个全等的等腰三角形，过点O作OM⊥AB，垂足为M，Rt△AOM中，易知
OM=OAcos∠AOM=Rcos∠AOB=Rcos×120°=Rcos60°，
AM=OAsin∠AOM=Rsin∠AOB=Rsin×120°=Rcos60°
∴AB=a=2AM=2Rsin60°
∴S_△AOB=AB×OM=×2Rsin60°•Rcos60°=R²sin60°cos60°
∴S_△ABC=3S_△AOB=3R²sin60°cos60°
∴a（h₁+h₂+h₃）=3R²sin60°cos60°
即：×2Rsin60°（h₁+h₂+h₃）=3R²sin60°cos60°
∴h₁+h₂+h₃=3Rcos60°
（2）如图②，五边形ABCDE是正五边形，半径是R，P是正五边形ABCDE内任意一点，P到五边形ABCDE各边距离分别为h₁、h₂、h₃、h₄、h₅，参照（1）的探索过程，确定h₁+h₂+h₃+h₄+h₅的值与正五边形ABCDE的半径R及中心角的关系．
（3）类比上述探索过程，直接填写结论
正六边形（半径是R）内任意一点P到各边距离之和 h₁+h₂+h₃+h₄+h₅+h₆=________
正八边形（半径是R）内任意一点P到各边距离之和 h₁+h₂+h₃+h₄+h₅+h₆+h₇+h₈=________
正n边形（半径是R）内任意一点P到各边距离之和 h₁+h₂+…+h_n=________．

如图，线段AD上有两点B、C，则图中共有线段

1. A.
   三条
2. B.
   四条
3. C.
   五条
4. D.
   六条

若代数式3x+4的值不大于0，则x的取值范围是

1. A.
   x＜-
2. B.
   x≤-
3. C.
   x＜
4. D.
   x≥

某超市购进了两批相同品种的水果，第一批用了2000元，第二批用了5500元．已知第二批购进水果的重量是第一批的2.5倍，且进价比第一批每千克多1元．设第一批购进水果的重量是x千克，请解答下列问题．
（1）第二批购进水果的重量是________千克；（用含x的代数式表示）
（2）求这两批水果共购进了多少千克？
（3）在这两批水果总重量正常损耗10%，其余全部售完的情况下，假设这两批水果的售价相同，即售价为每千克a元，且总利润率不低于26%，求a的大小．（提示：利润=售价-成本；利润率=×100%）

有一批货物，若月初出售可获得利润12万元，将本金和利润再投资经营，到月底可获得利润是投资数的3%；若月底出售可获得利润15万元，但需支付的储存费为货物成本的2%．
（1）假设这批货物的成本为x万元，用代数式表示两种出售方式月底的最终获利分别是多少？
（2）当成本在50万元到60万元之间时，哪种出售方式到月底最终获利要多？

∠α=40°，∠α的补角是∠β的2倍，则∠β为

1. A.
   20°
2. B.
   25°
3. C.
   80
4. D.
   70°

下列多项式相乘，能运用平方差公式的是

1. A.
   （1+x）（1+x）
2. B.
   （-a+b）（a-b）
3. C.
   （x+b）（b-x）
4. D.
   （x²-y）（y²+x）