
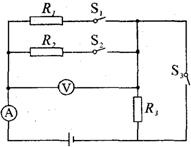
 育兴学校科技小组的同学们制作了一个多档位电热器模型.为了分析接入电路的电阻对电热器的电功率的影响,他们将电表接入电路中,其电路图如图所示.当只闭合开关S1时,电压表的示数为U1,电阻R3消耗的电功率为P3;当只闭合开关S2时,电压表的示数为U2,电阻R3消耗的电功率为P3′,测得此时电阻R2消耗的电功率为1.6W.已知2U1=U2,P3=4P3′,电源两端电压保持不变.
育兴学校科技小组的同学们制作了一个多档位电热器模型.为了分析接入电路的电阻对电热器的电功率的影响,他们将电表接入电路中,其电路图如图所示.当只闭合开关S1时,电压表的示数为U1,电阻R3消耗的电功率为P3;当只闭合开关S2时,电压表的示数为U2,电阻R3消耗的电功率为P3′,测得此时电阻R2消耗的电功率为1.6W.已知2U1=U2,P3=4P3′,电源两端电压保持不变.
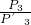 =
= =(
=(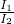 )2=
)2=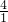 ,
,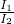 =
= ,
,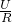 ,且U1:U2=1:2,
,且U1:U2=1:2,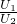 =
=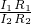 =
=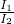 ×
×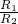 =
= ×
×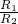 =
= ,
,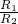 =
= ;
;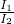 =
=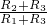 =
=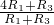 =
= ,
, =
=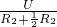 =
=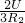 ,
,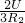 )2×R2=
)2×R2= ×
×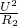 =1.6W,
=1.6W,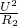 =3.6W,
=3.6W,
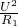 +
+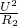 =
= +
+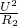 =5
=5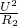 =5×3.6W=18W.
=5×3.6W=18W. 表示出R1和R2的电功率,两者之和即为最大总功率.
表示出R1和R2的电功率,两者之和即为最大总功率.

科目:初中物理 来源: 题型:
 (2007?门头沟区一模)育兴学校科技小组的同学们制作了一个多档位电热器模型.为了分析接入电路的电阻对电热器的电功率的影响,他们将电表接入电路中,其电路图如图所示.当只闭合开关S1时,电压表的示数为U1,电阻R3消耗的电功率为P3;当只闭合开关S2时,电压表的示数为U2,电阻R3消耗的电功率为P3′,测得此时电阻R2消耗的电功率为1.6W.已知2U1=U2,P3=4P3′,电源两端电压保持不变.
(2007?门头沟区一模)育兴学校科技小组的同学们制作了一个多档位电热器模型.为了分析接入电路的电阻对电热器的电功率的影响,他们将电表接入电路中,其电路图如图所示.当只闭合开关S1时,电压表的示数为U1,电阻R3消耗的电功率为P3;当只闭合开关S2时,电压表的示数为U2,电阻R3消耗的电功率为P3′,测得此时电阻R2消耗的电功率为1.6W.已知2U1=U2,P3=4P3′,电源两端电压保持不变.查看答案和解析>>
科目:初中物理 来源: 题型:
 (2007?大兴区一模)育兴学校科技小组的同学们制作了一个多档位电热器模型.为了分析接入电路的电阻对电热器的电功率的影响,他们将电表接入电路中,其电路图如图所示.电源两端电压不变,R1=10Ω.开关S1、S2都断开或都闭合所形成的两个电路状态中,电压表示数之比为1:6;R2消耗的最大功率和最小功率之比为4:1;R3的最小功率为0.8W.求:
(2007?大兴区一模)育兴学校科技小组的同学们制作了一个多档位电热器模型.为了分析接入电路的电阻对电热器的电功率的影响,他们将电表接入电路中,其电路图如图所示.电源两端电压不变,R1=10Ω.开关S1、S2都断开或都闭合所形成的两个电路状态中,电压表示数之比为1:6;R2消耗的最大功率和最小功率之比为4:1;R3的最小功率为0.8W.求:查看答案和解析>>
科目:初中物理 来源: 题型:解答题
 育兴学校科技小组的同学们制作了一个多档位电热器模型.为了分析接入电路的电阻对电热器的电功率的影响,他们将电表接入电路中,其电路图如图所示.电源两端电压不变,R1=10Ω.开关S1、S2都断开或都闭合所形成的两个电路状态中,电压表示数之比为1:6;R2消耗的最大功率和最小功率之比为4:1;R3的最小功率为0.8W.求:
育兴学校科技小组的同学们制作了一个多档位电热器模型.为了分析接入电路的电阻对电热器的电功率的影响,他们将电表接入电路中,其电路图如图所示.电源两端电压不变,R1=10Ω.开关S1、S2都断开或都闭合所形成的两个电路状态中,电压表示数之比为1:6;R2消耗的最大功率和最小功率之比为4:1;R3的最小功率为0.8W.求:查看答案和解析>>
科目:初中物理 来源:门头沟区一模 题型:问答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com