
【题目】设函数![]() ,
,![]() ,
,
(1)求曲线![]() 过原点的切线方程;
过原点的切线方程;
(2)设![]() ,若函数
,若函数![]() 的导函数
的导函数![]() 存在两个不同的零点
存在两个不同的零点![]() ,
,![]() ,求实数
,求实数![]() 的范围:
的范围:
(3)在(2)的条件下证明:![]()
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
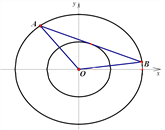
【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”.已知椭圆![]() ,以椭圆
,以椭圆![]() 的焦点为顶点作相似椭圆
的焦点为顶点作相似椭圆![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与椭圆
两点,且与椭圆![]() 仅有一个公共点,试判断
仅有一个公共点,试判断![]() 的面积是否为定值(
的面积是否为定值(![]() 为坐标原点)?若是,求出该定值;若不是,请说明理由.
为坐标原点)?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将直角三角形![]() 沿斜边上的高
沿斜边上的高![]() 折成
折成![]() 的二面角,已知直角边
的二面角,已知直角边![]() ,那么下面说法正确的是_________.
,那么下面说法正确的是_________.
(1) 平面![]() 平面
平面![]() (2)四面体
(2)四面体![]() 的体积是
的体积是![]()
(3)二面角![]() 的正切值是
的正切值是![]() (4)
(4)![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为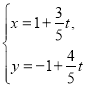 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
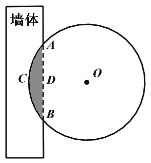
【题目】《九章算术》是我国古代著名数学经典,其中对勾股定理的论述,比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小;以锯锯之,深一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺,问这块圆柱形木料的直径是多少?长为0.5丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).己知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌墙内部分的体积约为( )(注:一丈=10尺=100寸,
寸,估算该木材镶嵌墙内部分的体积约为( )(注:一丈=10尺=100寸,![]() )
)
A.300立方寸B.305.6立方寸C.310立方寸D.316.6立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点,记以
两点,记以![]() ,
,![]() 为直径端点的圆为圆
为直径端点的圆为圆![]() .
.
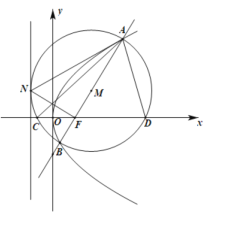
(1)证明:圆![]() 与抛物线的准线相切;
与抛物线的准线相切;
(2)设![]() ,点
,点![]() 在焦点的右侧,圆
在焦点的右侧,圆![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,记
两点,记![]() 和
和![]() 的面积为
的面积为![]() ,
,![]() 求
求![]() 的最大值(其中,点
的最大值(其中,点![]() 为圆
为圆![]() 与抛物线准线的切点)
与抛物线准线的切点)
查看答案和解析>>
科目:高中数学 来源: 题型:
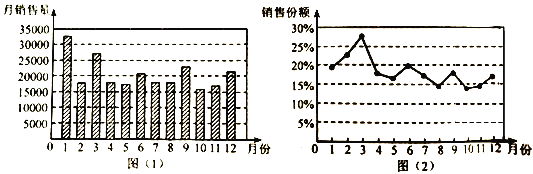
【题目】图(![]() )是某品牌汽车
)是某品牌汽车![]() 年月销量统计图,图(
年月销量统计图,图(![]() )是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
)是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
A.该品牌汽车![]() 年全年销量中,
年全年销量中,![]() 月份月销量最多
月份月销量最多
B.该品牌汽车![]() 年上半年的销售淡季是
年上半年的销售淡季是![]() 月份,下半年的销售淡季是
月份,下半年的销售淡季是![]() 月份
月份
C.![]() 年该品牌汽车所属公司
年该品牌汽车所属公司![]() 月份的汽车销量比
月份的汽车销量比![]() 月份多
月份多
D.该品牌汽车![]() 年下半年月销量相对于上半年,波动性小,变化较平稳
年下半年月销量相对于上半年,波动性小,变化较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com