练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
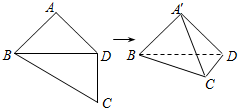
    6．如图，在四边形ABCD中，AB=AD=CD=1，BD=$\sqrt{2}$，BD⊥CD，将四边形ABCD沿对角线BD折成四面体A′BCD，使得平面A′BD⊥平面BDC，给出下列四个结论，其中正确的有（　　）
    A．A′B⊥CD
    B．四面体A′BCD的体积为$\frac{1}{2}$
    C．A′C与BD所成的角为60°
    D．四面体A′BCD的外接球的表面积为$\frac{7π}{2}$

    分析 利用平面与平面垂直的性质，可得CD⊥平面A′BD，即可得出结论．

    解答 解：∵BD⊥CD，平面A′BD⊥平面BDC，平面A′BD∩平面BDC=BD，
    ∴CD⊥平面A′BD，
    ∵A′B?平面A′BD，
    ∴A′B⊥CD，
    故选：A，

    点评 本题考查平面与平面垂直的性质，考查学生分析解决问题的能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．在空间直角坐标系Oxyz中，y釉上有一点M到已知点A（4，3，2）和B（2，5，2）的距离相等，则点M的坐标是（0，1，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．说明过A（2，0）平行于y轴的直线与方程|x|=2的关系．
    ①直线上的点的坐标是否都满足方程|x|=2？
    ②满足方程|x|=2的点是否都在直线上？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．方程5x-5-x+1+4=0的解集为{0}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知a=log52，b=log53，试用a，b表示log2740．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若角α，β的终边关于y轴对称，则α，β的 关系一定是（　　）
    A．α+β=πB．α-β=πC．α-β=（2k+1}π，k∈ZD．α+β=（2k+1}π，k∈Z

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．计算：
    （1）（lg5）2+lg2•lg5+lg2；
    （2）lg5（lg8+lg1000）+（lg2${\;}^{\sqrt{3}}$）2+lg0.06+lg$\frac{1}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．若角α是第一象限角，求下列各角终边所在位置．
    （1）$\frac{α}{2}$；
    （2）$\frac{α}{3}$；
    （3）2α；
    （4）180°+α

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知F1，F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的两个焦点，若双曲线上存在一点P，使得|PF1|，2a，|PF2|成等差数列，则双曲线离心率的取值范围是（　　）
    A．（1，2）B．（1，2]C．[2，+∞）D．（2，+∞）

    查看答案和解析>>

    同步练习册答案