
已知函数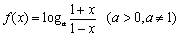
(1)求函数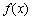 的定义域;
的定义域;
(2)判断函数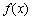 的奇偶性,并证明;
的奇偶性,并证明;
(3)求使 的
的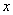 的取值范围.
的取值范围.
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
已知 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为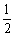 .
.
(1) 如果该同学10所高校的考试都参加, 试求恰有2所通过的概率;
(2) 假设该同学参加每所高校考试所需的费用均为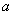 元. 该同学决定按
元. 该同学决定按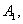
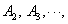
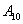 的顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试. 求该同学参加考试所需费用
的顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试. 求该同学参加考试所需费用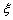 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于函数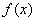 ,若存在
,若存在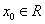 使得
使得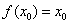 成立,则称
成立,则称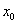 为
为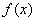 的不动点.
的不动点.
已知函数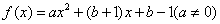 .
.
(1)若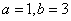 ,求函数
,求函数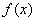 的不动点;
的不动点;
(2)若对任意实数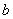 ,函数
,函数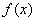 恒有两个相异的不动点,求
恒有两个相异的不动点,求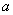 的取值范围;
的取值范围;
(3)在(2)的条件下,若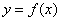 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数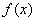 的不动点,且A、B两点关于直线
的不动点,且A、B两点关于直线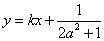 对称,求
对称,求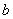 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省高三年级百强生竞赛文科数学试卷(解析版) 题型:解答题
记数列{an}的前n项和为Sn,若不等式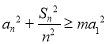 对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为 .
对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com