练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知m和n是两个正整数，m除以n的余数为r．
    （1）求证“K是m和n的公约数”的充要条件是“K是n和r的公约数”；
    （2）求2072与1064的公约数．

    分析 （1）已知m=np+r，若K是m和n的公约数，由r=m-np，则k必然是r的公约数，可得K是n和r的公约数．反之亦然．
    （2）利用“辗转相除法”即可得出；

    解答 （1）证明：已知m=np+r，
    若K是m和n的公约数，由r=m-np，则k必然是r的公约数，∴K是n和r的公约数．
    反之：若K是n和r的公约数，由m=np+r，则K必然是m的公约数，因此K是m和n的公约数．
    综上可得：“K是m和n的公约数”的充要条件是“K是n和r的公约数”．
    （2）解：2072=1064×1+1008，1064=1008×1+56，1008=56×18，
    ∴2072与1064的最大公约数是56．

    点评 本题考查了整除理论、充要条件、“辗转相除法”，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．某工厂统计资料显示，该厂生产的某种产品次品率p与日产量x（千克）（x∈N，且11≤x≤100）的关系如表，
    x11121314…99100
    p$\frac{2}{97}$ $\frac{1}{48}$ $\frac{2}{95}$ $\frac{1}{47}$  …$\frac{1}{9}$ $\frac{1}{4}$ 
    且已知每生产1千克正品盈利a元，每生产1千克次品损失$\frac{a}{2}$元（a＞0）．
    （1）写出生产该产品的日盈利额T（元）表示为日产量x的一个函数关系式；
    （2）为了获得最大盈利，该厂生产该产品的日产量应定为多少千克？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

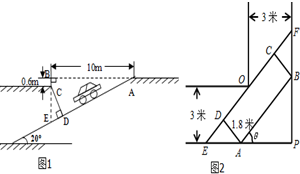    17．随着私家车的逐渐增多，居民小区“停车难”问题日益突出．本市某居民小区为缓解“停车难”问题，拟建造地下停车库，建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图．
    （1）按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图1示数据计算限定高度CD的值．（精确到0.1m）
    （下列数据提供参考：sin20°=0.3420，cos20°=0.9397，tan20°=0.3640）
    （2）在车库内有一条直角拐弯车道，车道的平面图如图2示，设∠PAB=θ（rad），车道宽为3米，现有一辆转动灵活的小汽车，其水平截面图为矩形，它的宽为1.8米，长为4.5米，问此车是否能顺利通过此直角拐弯车道？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

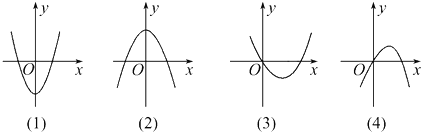
    14．如图，其中有一个是函数f（x）=$\frac{1}{3}$x3+ax2+（a2-1）x+1（a∈R，a≠0）的导函数f′（x）的图象，则f（-1）为（　　）
    A．2B．-$\frac{1}{3}$C．3D．-$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

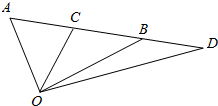    1．如图，已知$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AB}$，$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$，试用$\overrightarrow{OA}$，$\overrightarrow{OB}$表示$\overrightarrow{OC}$和$\overrightarrow{OD}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．化简下列各式：
    （1）2$\sqrt{3}$×$\root{3}{1.5}×\root{6}{12}$；
    （2）$\frac{{a}^{\frac{4}{3}}-8{a}^{\frac{1}{3}}b}{4{b}^{\frac{2}{3}}+2\root{3}{ab}+{a}^{\frac{2}{3}}}$$÷（1-2\root{3}{\frac{b}{a}}）×\root{3}{a}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．化简$\sqrt{2-2sinθ-co{s}^{2}θ}$的结果为1-sinθ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．求当k为何值时，关于x的方程$\frac{4k-3x}{k+2}$=2x的解为：
    （1）正数；
    （2）负数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=x2+ax+3．
    （1）若f（x）为偶函数，求实数a的值；
    （2）若f（x）在[1，+∞]内递增，求实数a的取值范围；
    （3）求f（x）在区间[0，2]上的最大值．

    查看答案和解析>>

    同步练习册答案