
| x | 11 | 12 | 13 | 14 | … | 99 | 100 |
| p | $\frac{2}{97}$ | $\frac{1}{48}$ | $\frac{2}{95}$ | $\frac{1}{47}$ | … | $\frac{1}{9}$ | $\frac{1}{4}$ |
分析 (1)根据表格,先确定p=$\frac{2}{108-x}$,x中次品有xp,正品有(x-xp),进而可得该厂日盈利额T关于日产量x的函数;
(2)利用基本不等式可确定函数的最值.
解答 解:(1)由题意知 p=$\frac{2}{108-x}$,x中次品有xp,正品有(x-xp)
所以该厂日盈利额T=a(x-xp)-$\frac{a}{2}$xp=a(x-$\frac{3p}{2}$x)=a(x-$\frac{3x}{108-x}$),(11≤x≤100,x∈N*)
(2)T=a(x-$\frac{3x}{108-x}$)=a[x-$\frac{3(x-108)+324}{108-x}$]=a(x+3-$\frac{324}{108-x}$)
=a(x-108+105-$\frac{324}{108-x}$)
=a[-(108-x)-$\frac{324}{108-x}$)+105]≤a[105+2$\sqrt{-(108-x)•(-\frac{324}{108-x}})$]=a(105+36)=141a
当且仅当-(108-x)=-$\frac{324}{108-x}$),即x=90,取等号
∵11≤x≤100,
∴x=90时,该厂盈利最大.
即为了获得最大盈利,该厂生产该产品的日产量应定为90千克.
点评 本题考查函数模型的构建,考查利用基本不等式求函数的最值,确定函数模型是关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:解答题
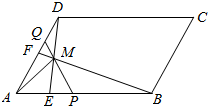 如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com