练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．从混有4件次品的20件商品中抽取3件，已知有1件是次品，求3件都是次品的概率．

    分析 先求出从混有4件次品的20件商品中抽取3件，基本事件总数，再求出有1件是次品，3件都是次品包含的基本事件个数，由此利用等可能事件概率计算公式能求出有1件是次品，3件都是次品的概率．

    解答 解：从混有4件次品的20件商品中抽取3件，已知有1件是次品，
    ∴抽取的3件产品中至少有一件是次品，基本事件总数n=${C}_{20}^{3}$-${C}_{16}^{3}$，
    有1件是次品，3件都是次品包含的基本事件个数m=${C}_{4}^{3}$，
    ∴有1件是次品，3件都是次品的概率p=$\frac{m}{n}$=$\frac{{C}_{4}^{3}}{{C}_{20}^{3}-{C}_{16}^{3}}$=$\frac{1}{145}$．

    点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．已知a，b是两条不同的直线．α，β，γ是三个不重合的平面，则下列命题为真命题的是（　　）
    A．若a∥α，α⊥β，则a⊥β
    B．若a，b与α所成角相等，则a∥b
    C．若α⊥β，γ⊥β，则α∥γ
    D．若a，b为异面直线，a?α，a∥β，b?β，b∥α，则α∥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某工厂统计资料显示，该厂生产的某种产品次品率p与日产量x（千克）（x∈N，且11≤x≤100）的关系如表，
    x11121314…99100
    p$\frac{2}{97}$ $\frac{1}{48}$ $\frac{2}{95}$ $\frac{1}{47}$  …$\frac{1}{9}$ $\frac{1}{4}$ 
    且已知每生产1千克正品盈利a元，每生产1千克次品损失$\frac{a}{2}$元（a＞0）．
    （1）写出生产该产品的日盈利额T（元）表示为日产量x的一个函数关系式；
    （2）为了获得最大盈利，该厂生产该产品的日产量应定为多少千克？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．
    从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本，监测值频数如茎叶图所示（十位为茎，个位为叶）：
    （I）求空气质量为超标的数据的平均数与方差；
    （II）从空气质量为二级的数据中任取2个，求这2个数据的和小于100的概率；
    （III）以这12天的PM2.5日均值来估计2012年的空气质量情况，估计2012年（366天）大约有多少天的空气质量达到一级或二级．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．△ABC的内角A、B、C的对边分别为a、b、c，且asinA+csinC-$\sqrt{2}$asinC=bsinB．则∠B=$\frac{π}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．为了让更多的人参与2010年在上海举办的“世博会”，上海某旅游公司面向国内外发行总量为2000万张的旅游优惠卡，其中向境外人士发行的是世博金卡（简称金卡），向境内人士发行的是世博银卡（简称银卡）．现有一个由36名游客组成的旅游团到上海参观旅游，其中$\frac{3}{4}$是境外游客，其余是境内游客．在境外游客中有$\frac{1}{3}$持金卡，在境内游客中有$\frac{2}{3}$持银卡．
    （I）在该团中随机采访3名游客，求恰有1人持金卡且持银卡者少于2人的概率；
    （Ⅱ）在该团的境内游客中随机采访3名游客，设其中持银卡人数为随机变量ξ，求ξ的分布列及数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

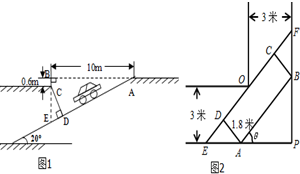    17．随着私家车的逐渐增多，居民小区“停车难”问题日益突出．本市某居民小区为缓解“停车难”问题，拟建造地下停车库，建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图．
    （1）按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图1示数据计算限定高度CD的值．（精确到0.1m）
    （下列数据提供参考：sin20°=0.3420，cos20°=0.9397，tan20°=0.3640）
    （2）在车库内有一条直角拐弯车道，车道的平面图如图2示，设∠PAB=θ（rad），车道宽为3米，现有一辆转动灵活的小汽车，其水平截面图为矩形，它的宽为1.8米，长为4.5米，问此车是否能顺利通过此直角拐弯车道？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

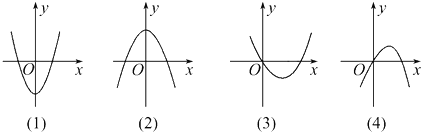
    14．如图，其中有一个是函数f（x）=$\frac{1}{3}$x3+ax2+（a2-1）x+1（a∈R，a≠0）的导函数f′（x）的图象，则f（-1）为（　　）
    A．2B．-$\frac{1}{3}$C．3D．-$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．求当k为何值时，关于x的方程$\frac{4k-3x}{k+2}$=2x的解为：
    （1）正数；
    （2）负数．

    查看答案和解析>>

    同步练习册答案