
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2+$\sqrt{10}$ | B. | 2+$\sqrt{7}$ | C. | 1+$\sqrt{10}$ | D. | 1+$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,α⊥β,则a⊥β | |
| B. | 若a,b与α所成角相等,则a∥b | |
| C. | 若α⊥β,γ⊥β,则α∥γ | |
| D. | 若a,b为异面直线,a?α,a∥β,b?β,b∥α,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 11 | 12 | 13 | 14 | … | 99 | 100 |
| p | $\frac{2}{97}$ | $\frac{1}{48}$ | $\frac{2}{95}$ | $\frac{1}{47}$ | … | $\frac{1}{9}$ | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
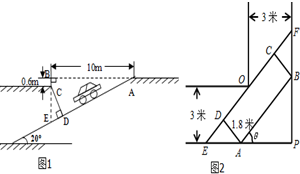 随着私家车的逐渐增多,居民小区“停车难”问题日益突出.本市某居民小区为缓解“停车难”问题,拟建造地下停车库,建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图.
随着私家车的逐渐增多,居民小区“停车难”问题日益突出.本市某居民小区为缓解“停车难”问题,拟建造地下停车库,建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com