
分析 由条件利用两个向量垂直的性质可得(3$\overrightarrow{a}+2\overrightarrow{b}$)•(λ$\overrightarrow{a}$-$\overrightarrow{b}$)=0,由此求得 λ的值.
解答 解:由题意(3$\overrightarrow{a}+2\overrightarrow{b}$)$⊥(λ\overrightarrow{a}-\overrightarrow{b})$可得(3$\overrightarrow{a}+2\overrightarrow{b}$)•(λ$\overrightarrow{a}$-$\overrightarrow{b}$)=3λ•${\overrightarrow{a}}^{2}$+(2λ-3)$\overrightarrow{a}•\overrightarrow{b}$-2${\overrightarrow{b}}^{2}$=12λ+(2λ-3)×0-2×9=0,∴λ=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题主要考查两个向量垂直的性质,两个向量的数量积的运算,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | b2-2a=0 | B. | b2+4a=0 | C. | b2+2a=0 | D. | b2-4a=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
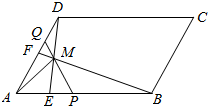 如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1(相关指数2为0.97) | B. | 模型2(相关指数R2为0.89) | ||
| C. | 模型3(相关指数R2为0.56 ) | D. | 模型4(相关指数R2为0.45) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com