Question

17．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2．|$\overrightarrow{c}$|=1.$\overrightarrow{a}$•$\overrightarrow{b}$=1，则（$\overrightarrow{a}$-$\overrightarrow{c}$）•（$\overrightarrow{b}$-$\overrightarrow{c}$）的最大值为 （　　）

• A． 2+$\sqrt{10}$
• B． 2+$\sqrt{7}$
• C． 1+$\sqrt{10}$
• D． 1+$\sqrt{7}$

Answer 1

分析 如图所示，设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角∠AOB=θ．根据|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，$\overrightarrow{a}$•$\overrightarrow{b}$=1，可得cosθ=$\frac{1}{4}$，sinθ=$\frac{\sqrt{15}}{4}$．则A（2，0），B$（\frac{1}{2}，\frac{\sqrt{15}}{2}）$．设C（cosα，sinα），代入（$\overrightarrow{a}$-$\overrightarrow{c}$）•（$\overrightarrow{b}$-$\overrightarrow{c}$）展开化简，利用和差公式、三角函数的单调性值域即可得出．

解答 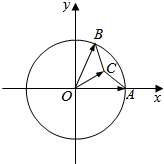解：如图所示，
设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角∠AOB=θ．
∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，$\overrightarrow{a}$•$\overrightarrow{b}$=1，
∴2×2cosθ=1，
∴cosθ=$\frac{1}{4}$，sinθ=$\frac{\sqrt{15}}{4}$．
则A（2，0），B$（\frac{1}{2}，\frac{\sqrt{15}}{2}）$．
设C（cosα，sinα），
则（$\overrightarrow{a}$-$\overrightarrow{c}$）•（$\overrightarrow{b}$-$\overrightarrow{c}$）=（2-cosα，-sinα）•$（\frac{1}{2}-cosα，\frac{\sqrt{15}}{2}-sinα）$
=$（2-cosα）（\frac{1}{2}-cosα）$$-sinα（\frac{\sqrt{15}}{2}-sinα）$
=$2-\frac{5}{2}cosα-\frac{\sqrt{15}}{2}sinα$
=2-$\sqrt{10}$$（\frac{\sqrt{6}}{4}sinα+\frac{\sqrt{10}}{4}cosα）$
=2-$\sqrt{10}$sin（α+φ）≤2+$\sqrt{10}$，当sin（α+φ）=-1时取等号．
故选：A．

点评 本题考查了向量数量积运算性质、和差公式、三角函数的单调性值域，考查了推理能力与计算能力，属于中档题