
【题目】若函数![]() 的图像上存在两点,使得函数的图像在这两点处的切线互相垂直,则称
的图像上存在两点,使得函数的图像在这两点处的切线互相垂直,则称![]() 具有
具有![]() 性质.下列函数中具有
性质.下列函数中具有![]() 性质的是( ).
性质的是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (t为参数).
(t为参数).
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的普通方程;
的普通方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,,求点
上一点,,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形![]() 中(图1),
中(图1),![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,使得
同侧折起,使得![]() ,
, ![]() ,得空间几何体
,得空间几何体![]() (图2).
(图2).
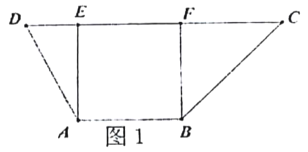
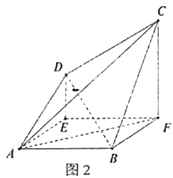
(1)证明: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】底面为菱形且侧棱垂直于底面的四棱柱![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,过点
的中点,过点![]() ,
, ![]() ,
, ![]() ,
, ![]() 的平面截直四棱柱
的平面截直四棱柱![]() ,得到平面四边形
,得到平面四边形![]() ,
, ![]() 为
为![]() 的中点,且
的中点,且![]() ,当截面的面积取最大值时,
,当截面的面积取最大值时, ![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
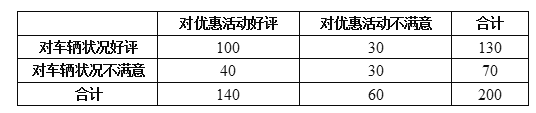
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过转赠给好友.某用户共获得了5张骑行券,其中只有2张是一元券.现该用户从这5张骑行券中随机选取2张转赠给好友,求选取的张中至少有1张是一元券的概率.
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过转赠给好友.某用户共获得了5张骑行券,其中只有2张是一元券.现该用户从这5张骑行券中随机选取2张转赠给好友,求选取的张中至少有1张是一元券的概率.
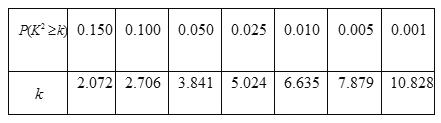
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】=2sin(ωx+φ),x∈R,其中ω>0,﹣π<φ≤π.若函数f(x)的最小正周期为6π,且当x=![]() 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
A. f(x)在区间[﹣2π,0]上是增函数B. f(x)在区间[﹣3π,﹣π]上是增函数
C. f(x)在区间[3π,5π]上是减函数D. f(x)在区间[4π,6π]上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业三月中旬生产A、B、C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
产品类别 | A | B | C |
产品数量(件) | 1 300 | ||
样本容量(件) | 130 |
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C的产品数量是( )
A.80B.800C.90D.900
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,过
,过![]() 作直线
作直线![]() 与边
与边![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .当直线
.当直线![]() 时,
时,![]() 值为
值为![]() ;当
;当![]() 为边
为边![]() 的中点时,
的中点时,![]() 值为
值为![]() .当
.当![]() ,
,![]() 变化时,记
变化时,记![]() (即
(即![]() 、
、![]() 中较大的数),则
中较大的数),则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com