练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设0≤θ＜2π，已知两个向量
    OP1
    =(cosθ，sinθ)，
    OP2
    =(2+sinθ，2-cosθ)    ，则向量
    P1P2
    长度的最大值是（　　）
    A、
    		2
    B、
    		3
    C、3
    		2
    D、2
    		3
    分析：根据向量的减法法则求出
    P1P2
    的坐标，利用向量模的坐标公式和同角平方关系，化简向量
    P1P2
    的模代数式，再根据已知角的范围和余弦函数性质，求出
    P1P2
    模的最大值．
    解答：解：由向量的减法知，
    P1P2
    =
    OP2
    -
    OP1
    =（2+sinθ-cosθ，2-cosθ-sinθ），
    ∴|
    P1P2
    |=
    		(2+sinθ-cosθ)2+(2-cosθ-sinθ)2

    =
    		4+4(sinθ-cosθ)+(sinθ-cosθ)2+4-4(sinθ+cosθ)+(cosθ+sinθ)2

    =
    		10-8cosθ
    ，
    ∵0≤θ＜2π，∴-1≤cosθ≤1，
    则当cosθ=-1时，
    P1P2
    的长度有最大值是3
    		2
    ．
    故选C．
    点评：本题考查了向量减法和向量模的坐标运算，利用了同角的平方关系和余弦函数的性质，考查了运用知识和解决问题的能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设0＜θ＜
    π
    2
    ，已知a1=2cosθ，an+1=
    		an+2
    (n∈N*)    ，猜想an=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设0＜θ＜
    π
    2
    ，已知a1=2cosθ，an+1=
    		2+an
    （n∈N*），通过计算数列{an}的前几项，猜想其通项公式为an=
    2cos
    θ
    2n-1
    2cos
    θ
    2n-1
    （n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    选修4-5：不等式选讲
    设函数f（x）=|2x+1|-|x-3|．
    （1）解不等式f（x）＞0；
    （2）已知关于x的不等式a+3＜f（x）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设0＜θ＜
    π
    2
    ，已知a1=2cosθ，an+1=
    		2+an
    （n∈N*），猜想an等于（　　）
    A、2cos
    θ
    2n
    B、2cos
    θ
    2n-1
    C、2cos
    θ
    2n+1
    D、2sin
    θ
    2n

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏五校高三下学期期初教学质量调研数学卷（解析版） 题型：解答题

    设非常数数列{an}满足an+2＝，n∈N*，其中常数α，β均为非零实数，且α＋β≠0.

    （1）证明：数列{an}为等差数列的充要条件是α＋2β＝0；

    （2）已知α＝1，β＝， a1＝1，a2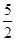＝，求证：数列{| an＋1－an－1|} (n∈N*，n≥2)与数列{n＋} (n∈N*)中没有相同数值的项.

     

    查看答案和解析>>

    同步练习册答案