
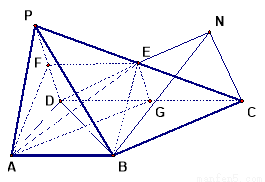
如图,四棱锥 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中 ,
,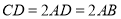 ,平面
,平面 底面
底面 ,
, 是
是 的中点.
的中点.

(1)求证: //平面
//平面 ;
;
(2)求 与平面BDE所成角的余弦值;
与平面BDE所成角的余弦值;
(3)线段PC上是否存在一点M,使得AM⊥平面PBD,如果存在,求出PM的长度;如果不存在,请说明理由。
(1)详见解析;(2)cos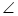 CBN=
CBN=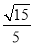 ;(3)不存在点M满足题意.
;(3)不存在点M满足题意.
【解析】
试题分析:(1)证明BE∥平面PAD,只需证明AF∥BE;
(2)过C作DE的垂线,交DE的延长线于N,连接BN,证明∠CBN就是直线BC与平面BDE所成角,从而可求BC与平面BDE所成角的余弦值;
(3)假设PC上存在点M,使得AM⊥平面PBD,则AM⊥PD,可得点M与E重合.取CD中点G,连接EG,AG,则BD⊥AG,证明PD⊥平面BCD,从而PD⊥AD,这与△PAD是等边三角形矛盾.
试题解析:(1)取PD中点F,连接AF, EF
则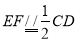 ,
,
又,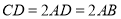
∴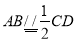
∴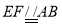
∴四边形ABEF是平行四边形 2分
∴AF∥BE 又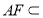 平面PAD,
平面PAD,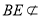 平面PAD
平面PAD
∴ //平面 4分
//平面 4分
(2)过C作DE的垂线,交DE的延长线于N,连接BN
∵平面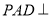 底面
底面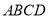 ,
,
∴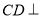 平面
平面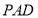
∴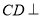 AF 又AF⊥PD,
AF 又AF⊥PD,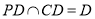
∴AF⊥平面PCD
∴BE⊥平面PCD
∴BE⊥CN,又CN⊥DE,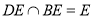
∴CN⊥平面BDE
∴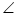 CBN就是直线与平面BDE所成角 7分
CBN就是直线与平面BDE所成角 7分
令AD=1,,易求得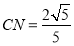 ,
,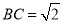
∴sin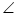 CBN=
CBN=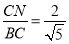
∴cos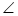 CBN=
CBN=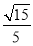
故与平面BDE所成角的余弦值为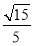 9分
9分
(3)假设PC上存在点M,使得AM⊥平面PBD 则AM⊥PD,由(2)AF⊥PD
∴PD⊥平面AFM,又PD⊥平面ABEF
故点M与E重合。 1分
取CD中点G,连接EG,AG
易证BD⊥AG,又BD⊥AE
∴BD⊥平面AEG
∴BD⊥EG
∴BD⊥PD,又PD⊥CD
∴PD⊥平面BCD
从而PD⊥AD,这与⊿PAD是等边三角形矛盾
(另解坐标法)
证明:取AD中点O,连接PO∵侧面PAD是等边三角形 ∴PO⊥AD
又∵平面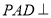 底面, ∴PO⊥平面ABCD 2分
底面, ∴PO⊥平面ABCD 2分
设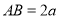 ,如图建立空间坐标系,则
,如图建立空间坐标系,则
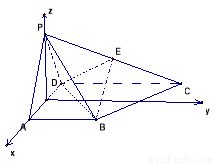
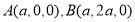 ,,
,,
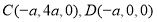 ,. 3分
,. 3分
(1)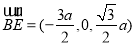 ,,
,,
所以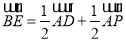 ,
,
∵平面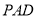 ,∴平面
,∴平面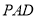 . 5分
. 5分
(2),
设平面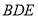 的一个法向量为
的一个法向量为
则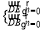 求得平面
求得平面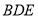 的一个法向量为; 7分
的一个法向量为; 7分
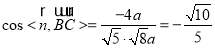 , 8分
, 8分
所以直线与平面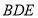 所成角的余弦值为。 10分
所成角的余弦值为。 10分
(3)设存在点M(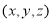 满足AM⊥平面PBD,则M、P、C三点共线
满足AM⊥平面PBD,则M、P、C三点共线
因为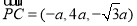 ,所以存在实数
,所以存在实数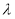 ,使得
,使得
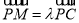 即
即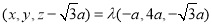 11分
11分
∵AM⊥平面PBD ∴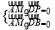 得
得 (不合题意)
(不合题意)
故在线段上不存在点M满足题意。 14分
考点:(1)空间的位置关系的证明;(2)线面角的求法;(3)向量在立体几何中的应用.


科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测文数学试卷(解析版) 题型:选择题
给出命题:“若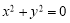 ,则
,则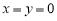 ”,在它的逆命题、否命题、逆否命题中,真命题的个数是
”,在它的逆命题、否命题、逆否命题中,真命题的个数是
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:2015届湖北孝感高级中学高二上学期期末考试文科数学试卷(解析版) 题型:选择题
函数y=f(x)在定义域(-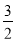 ,3)内的图像如图所示.记y=f(x)的导函数为y=f?(x),则不等式f?(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f?(x),则不等式f?(x)≤0的解集为( )
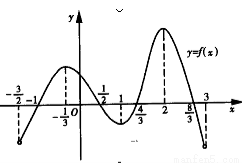
A.[-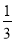 ,1]∪[2,3)
,1]∪[2,3)
B.[-1,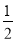 ]∪[
]∪[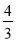 ,
,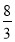 ]
]
C.[-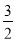 ,
,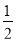 ]∪[1,2)
]∪[1,2)
D.(-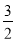 ,-
,-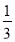 ]∪[
]∪[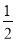 ,
,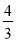 ]∪[
]∪[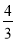 ,3)
,3)
查看答案和解析>>
科目:高中数学 来源:2015届浙江省台州市高二第一学期期末数学试卷(解析版) 题型:选择题
一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面直径与高的比是
A.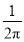 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届浙江温州十校联合体高二上学期期末联考理数学卷(解析版) 题型:填空题
过点P(3,4)的动直线与两坐标轴的交点分别为A、B,过A、B分别作两轴的垂线交于点M,则点M的轨迹方程是 。
查看答案和解析>>
科目:高中数学 来源:2015届浙江温州十校联合体高二上学期期末联考理数学卷(解析版) 题型:选择题
.设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届浙江温州十校联合体高二上学期期末联考文数学卷(解析版) 题型:选择题
若圆 上至少有三个不同的点到直线
上至少有三个不同的点到直线 的距离为
的距离为 ,则直线
,则直线 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com