
【题目】某个产品有若干零部件构成,加工时需要经过7道工序,分别记为![]() .其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系,若加工工序
.其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系,若加工工序![]() 必须要在工序
必须要在工序![]() 完成后才能开工,则称
完成后才能开工,则称![]() 为
为![]() 的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
工序 |
|
|
|
|
|
|
|
加工时间 | 3 | 4 | 2 | 2 | 2 | 1 | 5 |
紧前工序 | 无 |
| 无 |
|
|
|
|
现有两台性能相同的生产机器同时加工该产品,则完成该产品的最短加工时间是( )
(假定每道工序只能安排在一台机器上,且不能间断.)
A. 11个小时 B. 10个小时 C. 9个小时 D. 8个小时
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,其中
,其中![]() .函数
.函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为4.
与其相邻的最高点的距离为4.
(Ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)计算![]() 的值;
的值;
(Ⅲ)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间 [0,3] 上的零点个数.
在区间 [0,3] 上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )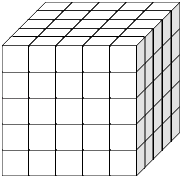
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足a1=2,an+1-an=3·22n-1.
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知a1=1, ![]() ,n∈N* .
,n∈N* .
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()

(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com