
【题目】下列函数既是奇函数,又在![]() 上单调递增的是
上单调递增的是![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题意,依次分析选项中函数的奇偶性以及![]() 上的单调性,综合即可得答案.
上的单调性,综合即可得答案.
根据题意,依次分析选项:
对于A,f(x)=|sinx|,为偶函数,不符合题意;
对于B,f(x)=ln![]() ,其定义域为(﹣e,e),有f(﹣x)=ln
,其定义域为(﹣e,e),有f(﹣x)=ln![]() ln
ln![]() f(x),为奇函数,
f(x),为奇函数,
设t![]() 1
1![]() ,在(﹣e,e)上为减函数,而y=lnt为增函数,
,在(﹣e,e)上为减函数,而y=lnt为增函数,
则f(x)=ln![]() 在(﹣e,e)上为减函数,不符合题意;
在(﹣e,e)上为减函数,不符合题意;
对于C,f(x)![]() (ex﹣e﹣x),有f(﹣x)
(ex﹣e﹣x),有f(﹣x)![]() (e﹣x﹣ex)
(e﹣x﹣ex)![]() (ex﹣e﹣x)=﹣f(x),为奇函数,且f′(x)
(ex﹣e﹣x)=﹣f(x),为奇函数,且f′(x)![]() (ex+e﹣x)>0,在R上为增函数,符合题意;
(ex+e﹣x)>0,在R上为增函数,符合题意;
对于D,f(x)=ln(![]() x),其定义域为R,
x),其定义域为R,
f(﹣x)=ln(![]() x)=﹣ln(
x)=﹣ln(![]() x)=﹣f(x),为奇函数,
x)=﹣f(x),为奇函数,
设t![]() x
x![]() ,y=lnt,t在R上为减函数,而y=lnt为增函数,
,y=lnt,t在R上为减函数,而y=lnt为增函数,
则f(x)=ln(![]() x)在R上为减函数,不符合题意;
x)在R上为减函数,不符合题意;
故选:C.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,![]() ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.

(1)求证:AC ⊥BC1;
(2)求证:AC 1 // 平面CDB1;
(3)(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
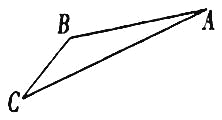
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱![]() 中的底面为等腰直角三角形,
中的底面为等腰直角三角形,![]() ,点
,点![]() 分别是边
分别是边![]() ,
,![]() 上动点,若直线
上动点,若直线![]() 平面
平面![]() ,点
,点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点的轨迹为
点的轨迹为![]()
![]()
A. 双曲线的一支![]() 一部分
一部分![]() B. 圆弧
B. 圆弧![]() 一部分
一部分![]()
C. 线段![]() 去掉一个端点
去掉一个端点![]() D. 抛物线的一部分
D. 抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】指出下列各题中p是q的什么条件.
(1)p:x-3=0,q:(x-2)(x-3)=0.
(2)p:两个三角形相似,q:两个三角形全等.
(3)p:a>b,q:ac>bc.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1且loga3>loga2,若函数f(x)=logax在区间[a,3a]上的最大值与最小值之差为1.
(1)求a的值;
(2)若1≤x≤3,求函数y=(logax)2-loga![]() +2的值域.
+2的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com