
(本题满分12分)在 中,内角
中,内角 对边的边长分别是
对边的边长分别是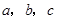 ,已知
,已知 ,
, ,
, ,求
,求 的面积.
的面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分) 如图,某观测站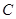 在城
在城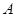 的南偏西
的南偏西 的方向上,由
的方向上,由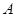 城出发有一公路,走向是南偏东
城出发有一公路,走向是南偏东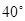 ,在
,在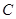 处测得距
处测得距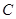 为31公里的公路上
为31公里的公路上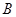 处,有一人正沿公路向
处,有一人正沿公路向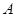 城走去,走了20公里后,到达
城走去,走了20公里后,到达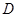 处,此时
处,此时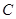 、
、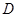 间距离为
间距离为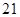 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达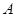 城.
城.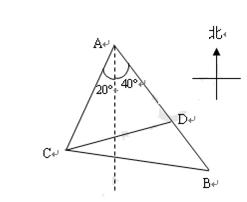
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
12分)某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇). 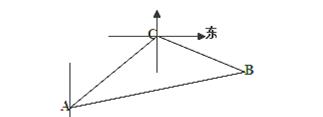
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com