
(本题满分12分)在 中,角
中,角 所对的边为
所对的边为 已知
已知 .
.
(1)求 值;(2)若
值;(2)若 面积为
面积为 ,且
,且 ,求
,求 值.
值.
(Ⅰ)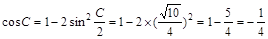 ;(Ⅱ)
;(Ⅱ)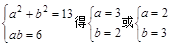 。
。
解析试题分析: (1)根据二倍角公式来得到角C的余弦值。
(2)在第二问中,结合三角形的面积公式,以及正弦定理,化角为边,然后得到边的关系,结合角C的余弦定理得到ab的值,进而解得。
解:(Ⅰ)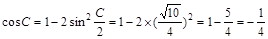 ……………………4分
……………………4分
(Ⅱ)∵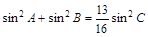 ,由正弦定理可得:
,由正弦定理可得: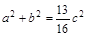
由(Ⅰ)可知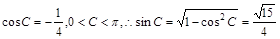 .
.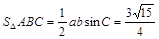 ,
,
得ab=6………………………………………………8分
由余弦定理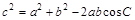
可得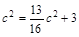
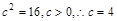 …………………………………………10分
…………………………………………10分
由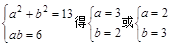 ……………12分
……………12分
考点:本题主要考查解三角形中正弦定理和余弦定理的运用,以及三角形的面积公式的综合运用问题。
点评:解决该试题的关键是就已知中关系式利用二倍角公式化简得到交C的余弦值,进而结合正弦定理得到a,b,c的平方关系,和余弦定理得到a,b的值。


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
本题满分10分)
一艘轮船按照北偏西50°的方向,以15海里每小时的速度航行,一个灯塔M原来在轮船的北偏东10°方向上,经过40分钟,轮船与灯塔的距离是 海里,则灯塔和轮船原来的距离为多少?
海里,则灯塔和轮船原来的距离为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)在 ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=
ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ,sinB=
,sinB= cosC.
cosC.
(Ⅰ)求tanC的值;
(Ⅱ)若a= ,求
,求 ABC的面积
ABC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com