练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知m、n、p、q均为正整数，现给出四个命题：①{an}为等差数列，若m+n=p+q,则am+an=ap+aq;②{an}为等比数列，若m+n=p+q，则am·an=ap·aq；③{an}为等差数列，则{a3n}也是等差数列；④{an}为等比数列，则{an+3}也是等比数列.

    其中正确的命题有(    )

    A.1个            B.2个              C.3个            D.4个

    解析：①②③④全部正确.

    答案：D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知两条互相平行的直线l1，l2之间的距离为常数a，这两条直线与边长为1的正方形的四条边分别交于点M，N，P，Q（按逆时针方向排列且均不与正方形的顶点重合）．
    （理科生做）试问是否存在常数a，使得四边形MNPQ的两条对角线的夹角θ为定值？若存在，求出所有的常数a及相应的θ的值；若不存在，说明理由．
    （文科生做）当a=
    		2
    2
    时，四边形MNPQ的两条对角线的夹角θ是否为定值？若是，求出θ的值；若不是，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数,且 w.w.w.k.s.5.u.c.o.m                                  

    (1) 试用含的代数式表示b,并求的单调区间；

    （2）令,设函数在处取得极值，记点M (,)，N(,)，P(),  ,请仔细观察曲线在点P处的切线与线段MP的位置变化趋势，并解释以下问题：

    （I）若对任意的m (, x)，线段MP与曲线f(x)均有异于M,P的公共点，试确定t的最小值，并证明你的结论；

    （II）若存在点Q(n ,f(n)), x n< m,使得线段PQ与曲线f(x)有异于P、Q的公共点，请直接写出m的取值范围（不必给出求解过程）w.w.w.k.s.5.u.c.o.m                                  

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数,且 

    (1) 试用含的代数式表示b,并求的单调区间；

    （2）令,设函数在处取得极值，记点M (,)，N(,)，P(),  ,请仔细观察曲线在点P处的切线与线段MP的位置变化趋势，并解释以下问题：

    （I）若对任意的m (, x)，线段MP与曲线f(x)均有异于M,P的公共点，试确定t的最小值，并证明你的结论；

    （II）若存在点Q(n ,f(n)), x n< m,使得线段PQ与曲线f(x)有异于P、Q的公共点，请直接写出m的取值范围（不必给出求解过程）

    查看答案和解析>>

    科目：高中数学 来源：2007-2008学年北京市海淀区高二（上）期中数学试卷（解析版） 题型：解答题

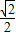    已知两条互相平行的直线l1，l2之间的距离为常数a，这两条直线与边长为1的正方形的四条边分别交于点M，N，P，Q（按逆时针方向排列且均不与正方形的顶点重合）．
    （理科生做）试问是否存在常数a，使得四边形MNPQ的两条对角线的夹角θ为定值？若存在，求出所有的常数a及相应的θ的值；若不存在，说明理由．
    （文科生做）当a=时，四边形MNPQ的两条对角线的夹角θ是否为定值？若是，求出θ的值；若不是，说明理由．

    查看答案和解析>>

    同步练习册答案