
(本小题满分12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某被邀请者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(Ⅱ)假定(Ⅰ)中被邀请到的3个人中恰有两人接受挑战.根据活动规定,现记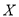 为接下来被邀请到的6个人中接受挑战的人数,求
为接下来被邀请到的6个人中接受挑战的人数,求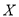 的分布列和均值(数学期望).
的分布列和均值(数学期望).
(Ⅰ)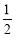 ;(Ⅱ)
;(Ⅱ)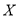 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
|
数学期望为3.
【解析】
试题分析:
解法一:(Ⅰ)此题可看做古典概率模型,列举法出3个人参与该项活动的可能结果和至少有2个人接受挑战的可能结果,即可求出(Ⅱ)每个人接受挑战的概率为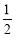 ,不接受挑战的概率也为
,不接受挑战的概率也为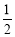 ,故
,故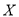 的可能取值为1,2,3,4,5,6,求出
的可能取值为1,2,3,4,5,6,求出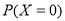 、
、
 、
、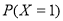 、
、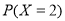 、
、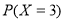 、
、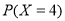 、
、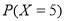 、
、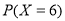 ,进而列出分布列,根据
,进而列出分布列,根据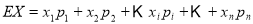 可得均值.
可得均值.
解法二:(Ⅰ)排列组合的方法,至少有2个人接受挑战分为两种情况,恰有两人接收挑战和恰有三人接收挑战,因而得到 (Ⅱ)由题意分析可知,
(Ⅱ)由题意分析可知, 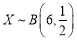 ,在
,在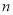 次独立重复试验中,事件发生
次独立重复试验中,事件发生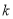 次的概率为
次的概率为 (
(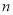 =6,
=6,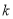 =1,2,3,4,5,6)可得
=1,2,3,4,5,6)可得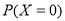 、
、
 、
、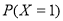 、
、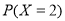 、
、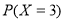 、
、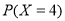 、
、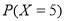 、
、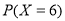 ,进而列出分布列,求均值见解法一.
,进而列出分布列,求均值见解法一.
试题解析:解法一:(Ⅰ)这3个人接受挑战分别记为 、
、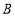 、
、 ,则
,则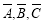 分别表示这3个人不接受挑战.这3个人参与该项活动的可能结果为:
分别表示这3个人不接受挑战.这3个人参与该项活动的可能结果为: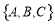 ,
,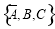 ,
,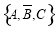 ,
,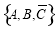 ,
,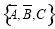 ,
,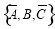 ,
,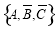 ,
,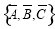 .共有8种; 2分
.共有8种; 2分
其中,至少有2个人接受挑战的可能结果有: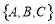 ,
,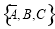 ,
,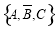 ,
,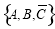 ,共有4种. 3分
,共有4种. 3分
根据古典概型的概率公式,所求的概率为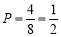 . 4分
. 4分
(说明:若学生先设“用 中的
中的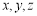 依次表示甲、乙、丙三人接受或不接受挑战的情况”,再将所有结果写成
依次表示甲、乙、丙三人接受或不接受挑战的情况”,再将所有结果写成 ,
, ,
,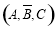 ,
,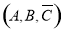 ,
,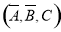 ,
,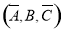 ,
,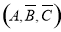 ,
,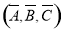 ,不扣分.)
,不扣分.)
(Ⅱ)因为每个人接受挑战与不接受挑战是等可能的,
所以每个人接受挑战的概率为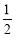 ,不接受挑战的概率也为
,不接受挑战的概率也为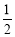 . 5分
. 5分
所以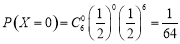 ,
,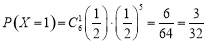 ,
,
 ,
,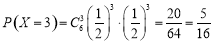 ,
,
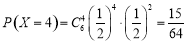 ,
,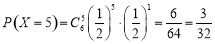 ,
,
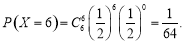 9分
9分
故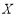 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
|
所以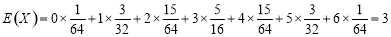 .
.
故所求的期望为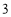 . 12分
. 12分
解法二:因为每个人接受挑战与不接受挑战是等可能的,
所以每个人接受挑战的概率为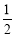 ,不接受挑战的概率也为
,不接受挑战的概率也为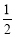 . 1分
. 1分
(Ⅰ)设事件M为“这3个人中至少有2个人接受挑战”,
则 . 4分
. 4分
(Ⅱ)因为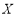 为接下来被邀请的6个人中接受挑战的人数,所以
为接下来被邀请的6个人中接受挑战的人数,所以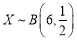 . 5分
. 5分
所以 ,
,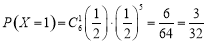 ,
,
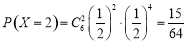 ,
,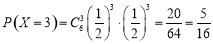 ,
,
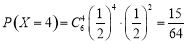 ,
,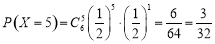 ,
,
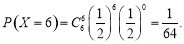 9分
9分
故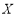 的分布列为: 10分
的分布列为: 10分
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
|
所以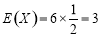 .故所求的期望为
.故所求的期望为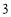 . 12分
. 12分
考点:1、古典概型;2、离散型随机变量;3、二项分布;4、均值.


科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知椭圆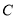 :
: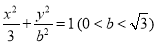 ,其通径(过焦点且与x轴垂直的直线被椭圆截得的线段)长
,其通径(过焦点且与x轴垂直的直线被椭圆截得的线段)长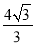 .
.
(1)求椭圆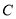 的方程;
的方程;
(2)设过椭圆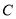 右焦点的直线(不与
右焦点的直线(不与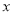 轴重合)与椭圆交于
轴重合)与椭圆交于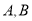 两点,问在
两点,问在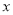 轴上是否存在一点
轴上是否存在一点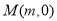 ,使
,使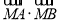 为常数?若存在,求点
为常数?若存在,求点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检理科数学试卷(解析版) 题型:选择题
4名考生在三道选做题中任选一道进行做答,则这三道题都有人选做的概率为( )
A.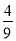 B.
B.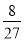 C.
C.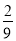 D.
D.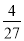
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,输出的x值为( ).
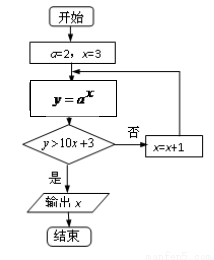
A.7 B.6 C.5 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知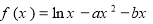 .
.
(1)若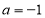 ,函数
,函数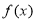 在其定义域内是增函数,求
在其定义域内是增函数,求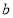 的取值范围;
的取值范围;
(2) 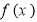 的图象与
的图象与 轴交于
轴交于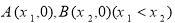 )两点,
)两点,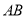 中点为
中点为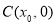 ,求证:
,求证: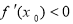 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷(解析版) 题型:填空题
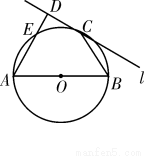
如图,圆O的直径AB = 8,C为圆周上一点,BC = 4,过C作圆的切线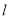 ,过A作直线
,过A作直线 的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为 .
的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷(解析版) 题型:选择题
如下图,在△OAB中,P为线段AB上的一点,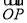 =x
=x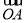 +y
+y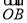 ,且
,且 =3
=3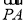 ,则( ).
,则( ).
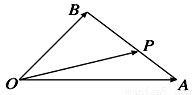
A、x=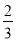 ,y=
,y=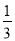 B、x=
B、x=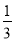 ,y=
,y=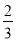
C、x=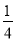 ,y=
,y= D、x=
D、x=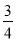 ,y=
,y=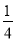
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省毕业生二月调研考试文科数学试卷(解析版) 题型:选择题
把函数 的图象向右平移
的图象向右平移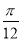 ,得到函数
,得到函数 的图象,则函数
的图象,则函数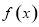 为( )
为( )
A.周期为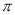 的奇函数 B.周期为
的奇函数 B.周期为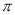 的偶函数
的偶函数
C.周期为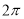 的奇函数 D.周期为
的奇函数 D.周期为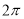 的偶函数
的偶函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com