
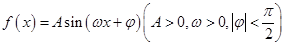 的图象与y轴的交点为
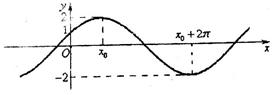
的图象与y轴的交点为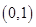 ,它在y轴右侧的第一个最高点和第一个最低点的坐标分别为
,它在y轴右侧的第一个最高点和第一个最低点的坐标分别为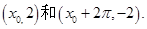
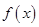 的解析式及
的解析式及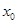 的值;
的值;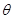 满足
满足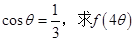 的值.
的值. 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源:不详 题型:解答题
 .
. 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);| | | | | | |
| | | | | | |
| | | | | | |

 的单调递增区间;
的单调递增区间; 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
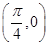 对称,则在区间[0,2π]上满足f(x)≤g(x)的x的范围是( ).
对称,则在区间[0,2π]上满足f(x)≤g(x)的x的范围是( ).A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ”的( ).
”的( ).| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 )的部分图象如图所示,则ω,φ的值分别为( ).
)的部分图象如图所示,则ω,φ的值分别为( ).
| A.2,0 | B.2, | C.2,- | D.2, |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 +2cos2x-1(x∈R).
+2cos2x-1(x∈R). ,b,a,c成等差数列,且
,b,a,c成等差数列,且 ·
· =9,求a的值.
=9,求a的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
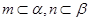 ,
,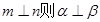 ;
; 是周期为2
是周期为2 的偶函数;
的偶函数; 的焦点为F,点P为抛物线上任意一点,则
的焦点为F,点P为抛物线上任意一点,则 的最小值为2;
的最小值为2;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com