
 ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C. ,0),证明:
,0),证明: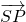 •
•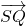 为定值.
为定值. ,
,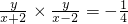 ,
, (x≠±2)
(x≠±2) ),Q(-1,-
),Q(-1,- ),若S(-
),若S(- ,0),
,0),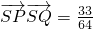 .
.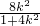 ,x1+x2=
,x1+x2=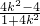
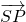 =(x1+
=(x1+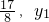 ),
),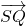 =(x2+
=(x2+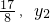 ),
), =(x1+
=(x1+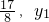 )•(x2+
)•(x2+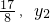 )=
)=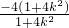 +
+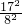 =
=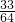 .
. ,建立方程,化简可得结论;
,建立方程,化简可得结论; ),Q(-1,-
),Q(-1,- ),可得
),可得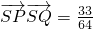 ;当动直线l的斜率存在时,设动直线l的方程联立方程组,消去y得一元二次方程,利用韦达定理及向量的数量积运算,可得结论.
;当动直线l的斜率存在时,设动直线l的方程联立方程组,消去y得一元二次方程,利用韦达定理及向量的数量积运算,可得结论. ,进而确定定值.
,进而确定定值. 

科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.| 3 |
| 5 |
| 12 |
| 13 |
| 3 |
| 2 |
| OA |
| OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com