
在Rt△ABO中,∠BOA=90°,|OA|=8,|OB|=6.已知P是Rt△ABO的内切圆![]() 上的任意一点,求点P到各顶点A,B,O距离的平方和的最大值与最小值.
上的任意一点,求点P到各顶点A,B,O距离的平方和的最大值与最小值.
解:如图所示,以OA,OB所在的直线分别为x轴、y轴,建立平面直角坐标系,则有A(8,0),B(0,6).
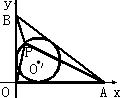
在Rt△ABO中,由勾股定理,得|AB|=10.
设圆![]() 的半径长为r,
的半径长为r,
由面积公式,可得S△ABO=![]() |OB|·|OA|=
|OB|·|OA|=![]() (|OA|·r+|OB|·r+|AB|·r),
(|OA|·r+|OB|·r+|AB|·r),
即48=24r,解得r=2.
所以圆![]() 的方程为(x-2)2+(y-2)2=4.
的方程为(x-2)2+(y-2)2=4.
设点P的坐标为(a,b)(0≤a≤4,0≤b≤4),
则有(a-2)2+(b-2)2=4,即a2+b2=4a+4b-4.
所以d2=|PA|2+|PB|2+|OP|2=(a-8)2+b2+a2+(b-6)2+a2+b2=88-4a(0≤a≤4).
所以(d2)max=88-4×0=88,(d2)min=88-4×4=72.
点评:在解平面几何题时,若遇到一些复杂的问题,可建立平面直角坐标系,简化思路.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:044
在
Rt△ABO中,∠BOA=90°,|OA|=8,|OB|=6,点P为它的内切圆C上任一点,求点P到顶点A、B、O的距离的平方和的最大值和最小值.查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
在Rt△ABO中,∠BOA=90°,|OA|=8,|OB|=6,点P为它的内切圆C上任一点,求点P到顶点A、B、O的距离的平方和的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com