Question

在Rt△ABO中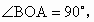，点P为它的内切圆C上任一点，求点P到顶点A、B、O的距离的平方和的最大和最小值．

Answer 1

答案：最大值88,最小值72
解析：

解：以O为坐标原点，OA所在直线为x轴，OB所在的直线为y轴建立平面直角坐标系，如图所示． 则A(8，0)，B(0，6)， 设△ABO的内切圆半径为r，则 易知，此时圆心C的坐标为C(2，2)． ∴△ABO的内切圆的方程为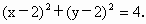 设P(x，y)为圆上任一点，点P到顶点A、B、O的距离的平方和为d，则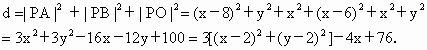 ∵点P(x，y)在圆上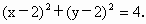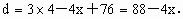，∴∴ ∵点P(x，y)是圆C上的任意点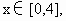，∴ ∴当x=0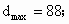时，当x=4时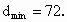， 求解最值问题时，应根据条件确定出它的函数关系(选择好自变量是顺利地解决问题的关键)．本题可求出三角形ABO的内切圆的方程，根据点P在所求的圆上，变成了一个条件最值问题来求解．