
设数列{ }满足:a1=2,对一切正整数n,都有
}满足:a1=2,对一切正整数n,都有
(1)探讨数列{ }是否为等比数列,并说明理由;
}是否为等比数列,并说明理由;
(2)设
(1)是,理由见解析;(2)证明过程详见解析.
解析试题分析:本题主要考查等比数列的定义、等比数列的证明、数学归纳法、放缩法等数学知识,考查学生的分析问题解决问题的能力、转化能力和计算能力.第一问,通过对已知表达式的移项,变形可得出数列的通项 ,可以用等比数列的定义证明也可以用数学归纳法证明;第二问,将第一问的结论代入,得到
,可以用等比数列的定义证明也可以用数学归纳法证明;第二问,将第一问的结论代入,得到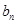 表达式,法一:利用放缩法和裂项相消法证明,法二:利用数列的累加法和放缩法证明.
表达式,法一:利用放缩法和裂项相消法证明,法二:利用数列的累加法和放缩法证明.
试题解析:⑴由 得
得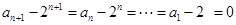 ,
,
∴对一切 ,可知
,可知 是首项为
是首项为 ,公比为
,公比为 的等比数列. 5分
的等比数列. 5分
(通过归纳猜想,使用数学归纳法证明的,亦应给分)
(2)由(1)知 6分
6分
证一:
 10分
10分 12分
12分
证二:∵ ≥
≥ (仅当
(仅当 时等号成立),故此,
时等号成立),故此, ≤
≤ 10分
10分
从而,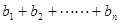 ≤
≤
 <
< 12分
12分
考点:1.数学归纳法;2.累加法;3.放缩法.


科目:高中数学 来源: 题型:解答题
某同学在一次研究性学习中发现以下四个不等式都是正确的: ;
; ;
; ;
; .
.
请你观察这四个不等式:
(1)猜想出一个一般性的结论(用字母表示);
(2)证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com