Question

在等差数列{a_n}中，若S₂≥4，S₃≤9，则a₄的最大值为________．

Answer 1

7
分析：设等差数列{a_n}的首项和公差分别为：a₁和d，可得求和公式，进而可得2a₁+d≥4，3a₁+3d≤9，而a₄=a₁+3d=-2（2a₁+d）+（3a₁+3d），代入可得．
解答：设等差数列{a_n}的首项和公差分别为：a₁和d，
由求和公式可得，
故有S₂=2a₁+d≥4，S₃=3a₁+3d≤9，
所以-2（2a₁+d）≤-8，
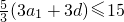
故a₄=a₁+3d=-2（2a₁+d）+（3a₁+3d）≤7
故答案为：7
点评：本题考查等差数列的求和公式和整体代入法求解式子的取值范围，属基础题．