Question

P为抛物线y²=4x上一动点，则点P到y轴距离和到点A（2，3）距离之和的最小值等于________．

Answer 1

分析：先求出抛物线的准线方程，焦点坐标，由于A在抛物线的外部，所以连接焦点F和点A，AF与抛物线的交点P，即为所求点，利用抛物线的定义可求点P到y轴距离和到点A（2，3）距离之和的最小值．
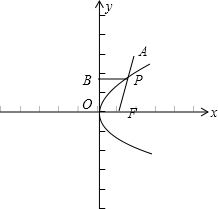
解答：解：y²=4x的准线是x=-1．抛物线的焦点坐标为（1，0）
由于A在抛物线的外部，所以连接焦点F和点A，AF与抛物线的交点P，即为所求点，
∵P到x=-1的距离等于P到焦点F的距离，
∴点P到y轴距离和到点A（2，3）距离之和为P到焦点F的距离
和到点A（2，3）距离之和减1，
∴当且仅当A，P，F三点共线时，点P到y轴距离和到点A（2，3）距离之和最小
∴点P到y轴距离和到点A（2，3）距离之和的最小值为|AF|-1=
故答案为：
点评：本题以抛物线的标准方程为载体，考查抛物线的定义，考查距离和，解题的关键是利用抛物线上的点到焦点的距离等于它到准线的距离．