练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆锥曲线C经过定点P（3，），它的一个焦点为F（1，0），对应于该焦点的准线为x=－1，斜率为2的直线交圆锥曲线C于A、B两点，且 AB =，求圆锥曲线C和直线的方程。

    【答案】圆锥曲线C的方程为y2=4x，直线的方程为y=2x－4.

    【解析】

    根据焦点和准线判断出曲线为抛物线，由此写出抛物线的方程.设出直线的方程斜截式，利用弦长公式和弦长列方程，解方程求得直线的截距.由此求得直线的方程.

    由于曲线的焦点对应的数量是，而准线对应的数量是，故猜想曲线是抛物线，根据，求得，故抛物线的方程是，将代入得，符合题意，故曲线的方程是.由于直线的斜率为，故可设直线的方程为，代入抛物线方程并化简得，故，所以，解得，故直线的方程是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一个总体分为A，B两层，其个体数之比为5：1，用分层抽样方法从总体中抽取一个容量为12的样本，已知B层中甲、乙都被抽到的概率为 ，则总体中的个数为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线与直线交于两点，

    （Ⅰ）当时，求在点和处的切线方程；

    （Ⅱ）若轴上存在点，当变动时，总有,试求出坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过抛物线y2＝2px(p＞0)的焦点F的直线l与抛物线交于B，C两点，l与抛物线的准线交于点A，且|AF|＝6，＝2，

    （1）求抛物线方程.

    （2）求|BC|.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=8a2lnx+x2+6ax+b（a，b∈R）
    （1）若曲线y=f（x）在点（1，f（1））处的切线方程为y=2x，求a，b的值；
    （2）若a≥1，证明：x1 ， x2∈（0，+∞），且x1≠x2 ， 都有 ＞14成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校在2012年的自主招生考试成绩中随机抽取100名中学生的笔试成绩，按成绩分组，得到的频率分布表如下所示.

    组号

    分组

    频数

    频率

    第1组

    [160,165)

    5

    0.050

    第2组

    [165,170)

    ①

    0.350

    第3组

    [170,175)

    30

    ②

    第4组

    [175,180)

    20

    0.200

    第5组

    [180,185)

    10

    0.100

    合计

    100

    1.00

    （1）请先求出频率分布表中①、②位置的相应数据，再完成频率分布直方图，并从频率分布直方图中求出中位数（中位数保留整数）；

    （2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，从这6名学生中随机抽取2名学生接受A考官进行面试，求：第4组至少有一名学生被考官A面试的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学生对其亲属30人的饮食习惯进行了一次调查，并用下图所示的茎叶图表示30人的饮食指数．(说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主)

    (1)根据以上数据完成下面的2×2列联表：

    主食 蔬菜

    主食 肉类

    总计

    50岁以下

    50岁以上

    总计

    (2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”？并写出简要分析．

    附参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）是定义在（0，+∞）上的单调函数，且对任意的x∈（0，+∞），都有f[f（x）﹣log2x]=3，则方程f（x）﹣f′（x）=2的解所在的区间是（ ）
    A.（0， ）
    B.（ ，1）
    C.（1，2）
    D.（2，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．
    （Ⅰ）证明：平面ACD⊥平面ABC；
    （Ⅱ）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C的余弦值．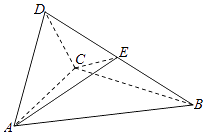

    查看答案和解析>>

    同步练习册答案