
【题目】抛物线y2=2px(p>0)的焦点为F,已知A,B为抛物线上的两个动点,且满足∠AFB=120°,过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则 ![]() 的最大值为( )
的最大值为( )
A.2
B.![]()
C.1
D.![]()
【答案】D
【解析】解:设|AF|=a,|BF|=b,连接AF、BF, 由抛物线定义,得|AF|=|AQ|,|BF|=|BP|,
在梯形ABPQ中,2|MN|=|AQ|+|BP|=a+b.
由余弦定理得,
|AB|2=a2+b2﹣2abcos120°=a2+b2+ab,
配方得,|AB|2=(a+b)2﹣ab,
又∵ab≤( ![]() )2 ,
)2 ,
∴(a+b)2﹣ab≥(a+b)2﹣ ![]() (a+b)2=
(a+b)2= ![]() (a+b)2
(a+b)2
得到|AB|≥ ![]() (a+b).
(a+b).
所以 ![]() ≤
≤ 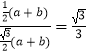 ,
,
即 ![]() 的最大值为
的最大值为 ![]() .
.
故选:D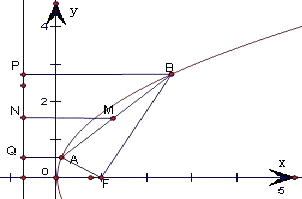
设|AF|=a,|BF|=b,连接AF、BF.由抛物线定义得2|MN|=a+b,由余弦定理可得|AB|2=(a+b)2﹣ab,进而根据基本不等式,求得|AB|的取值范围,从而得到本题答案.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,四个顶点构成的菱形的面积是4,圆
,四个顶点构成的菱形的面积是4,圆![]() 过椭圆
过椭圆![]() 的上顶点
的上顶点![]() 作圆
作圆![]() 的两条切线分别与椭圆
的两条切线分别与椭圆![]() 相交于
相交于![]() 两点(不同于点
两点(不同于点![]() ),直线
),直线![]() 的斜率分别为
的斜率分别为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 变化时,①求
变化时,①求![]() 的值;②试问直线
的值;②试问直线![]() 是否过某个定点?若是,求出该定点;若不是,请说明理由.
是否过某个定点?若是,求出该定点;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣ ![]() (a,b∈N*),f(1)=
(a,b∈N*),f(1)= ![]() 且f(2)<2.
且f(2)<2.
(1)求a,b的值;
(2)判断并证明函数y=f(x)在区间(﹣1,+∞)上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在点(1,f(1))处的切线与x轴平行.
在点(1,f(1))处的切线与x轴平行.
(Ⅰ)求实数a的值及f(x)的极值;
(Ⅱ)是否存在区间(t,t+ ![]() )(t>0),使函数f(x)在此区间上存在极值和零点?若存在,求实数t的取值范围,若不存在,请说明理由;
)(t>0),使函数f(x)在此区间上存在极值和零点?若存在,求实数t的取值范围,若不存在,请说明理由;
(Ⅲ)如果对任意的 ![]() ,有|f(x1)﹣f(x2)|≥k|
,有|f(x1)﹣f(x2)|≥k| ![]() |,求实数k的取值范围.
|,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x﹣ ![]() ,且f(2)=
,且f(2)= ![]() .
.
(1)求实数a的值;
(2)判断该函数的奇偶性;
(3)判断函数f(x)在(1,+∞)上的单调性,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知2Sn=3n+3.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足anbn=log3an , 求{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com