

(2)如图,地球上有两点A、B,A在东经13°,北纬30°,B在东经73°,北纬45°.试求A、B两点间的球面距离(设地球半径为R).
解析:利用地球的经度和纬度分别求出小圆的半径和有关角度.纬度是指OA与赤道面所成的线面角,而经度是指经过这点的经线与地轴确定的半平面与0°经线及地轴确定的半平面所成的二面角.第(2)题是球面距离,首先要计算A、B两点所对应的大圆圆心角AOB的度数.

(1)∵OA与赤道所在平面成30°角,?
∴∠AOO′=90°-30°=60°.?
∴AO′=R·sin60°=![]() R,l=r·θ=AO′·
R,l=r·θ=AO′·![]() R.?
R.?
(2)过A、B两点作赤道平面的射影A′、B′.连结AB,A′B′,?
∵Rt△OBB′,OB与赤道成45°角,?
∴B′O=cos45°·R=![]() R.?
R.?
同理,可得A′O=cos30°·R=![]() R.?
R.?
cos∠A′OB′=![]() .?
.?
A′B′=![]()
=![]()
=![]() .?
.?
过A点作AB″⊥BB′交BB′于B″.?
∵AA′∥BB′,AB″⊥BB′,∴AB″⊥AA′.?
∴AB″∥A′B′.∴AA′B′B″是矩形.?
由Rt△ABB″,得AB2=AB″2+BB″2.?
BB″=(![]() -
-![]() )R,AB″=A′B′.?
)R,AB″=A′B′.?
∴AB2=(![]() )R2.?
)R2.?
cos∠AOB=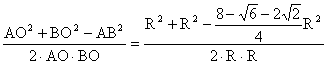
=![]() .?
.?
L=R·θ=R·arccos![]() .
.


科目:高中数学 来源: 题型:
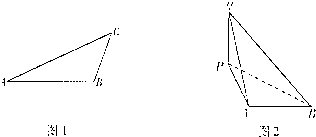 某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.
某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东![]() 方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s。
方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s。
(I)求A、C两上救援中心的距离;
(II)求P相对A的方向角;
(III)试分析信号分别从P点处和P点的正上方Q点(如图2,返回仓经Q点垂直落至P点)处发出时,A、B两个救援中心收到信号的时间差的变化情况(变大还是变小),并证明你的结论。

查看答案和解析>>
科目:高中数学 来源:2011年福建省福州三中高三练习数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com