
已知三条直线 :2x-y+a=0(a>0),直线
:2x-y+a=0(a>0),直线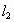 :4x-2y-1=0和直线
:4x-2y-1=0和直线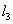 :x+y-1=0,且
:x+y-1=0,且 和
和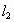 的距离是
的距离是 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到 的距离是P到
的距离是P到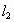 的距离的
的距离的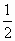 ;③P点到
;③P点到 的距离与P点到
的距离与P点到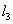 的距离之比是
的距离之比是 ;若能,求P点坐标;若不能,说明理由.
;若能,求P点坐标;若不能,说明理由.
|
(1) 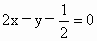 , ,
∴  与 与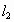 的距离 的距离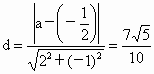 , ,
∴ 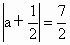 ,∴a>0,∴a=3. ,∴a>0,∴a=3.
(2) 设点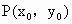 ,若P点满足条件②,则P点在与 ,若P点满足条件②,则P点在与 , ,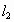 平行的直线 平行的直线 :2x-y+c=0上, :2x-y+c=0上,
且  即 即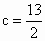 或 或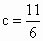 , ,
∴ 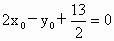 或 或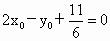 . .
若 P满足条件③,由点到直线的距离公式
∴ 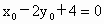 或 或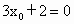 . .
由 P在第一象限,∴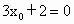 (不合). (不合).
联立方程 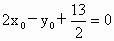 和 和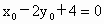 , ,
解得  , ,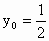 应舍去, 应舍去,
由 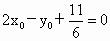 与 与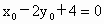 联立,解得 联立,解得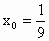 , ,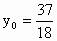 . .
∴ 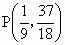 即为同时满足三个条件的点. 即为同时满足三个条件的点.
|
|
求解本题运用:平行直线间的距离公式和点到直线的距离公式. 一般地,对于平行线Ax+By+ |


科目:高中数学 来源: 题型:
(1)求实数a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到直线l1的距离是P点到直线l2的距离的![]() ;③P点到直线l1的距离与P点到直线l3的距离之比为
;③P点到直线l1的距离与P点到直线l3的距离之比为![]() ∶
∶![]() .若能,求出点P的坐标;若不能,请说明理由.
.若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知三条直线l1:2x-y+3=0,直线l2:-4x+2y+1=0和直线l3:x+y-1=0.能否找到一点P,使得P点同时满足下列三个条件:(1)P是第一象限的点;(2)P点到l1的距离是P点到l2的距离的![]() ;(3)P点到l1的距离与P点到l3的距离之比是
;(3)P点到l1的距离与P点到l3的距离之比是![]() .若能,求P点坐标;若不能,请说明理由.
.若能,求P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求a的值.
(2)求l3到l1的角θ.
(3)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l1的距离是P点到l2的距离的![]() ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是![]() ∶
∶![]() ?若能,求P点坐标;若不能,请说明理由.
?若能,求P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求a的值;
(2)求l3到l1的角θ;
(3)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l1的距离是P点到l2的距离的![]() ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是![]() ∶
∶![]() .若能,求出P点坐标;若不能,请说明理由.
.若能,求出P点坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com