
【题目】已知函数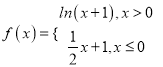 ,若
,若![]() ,且
,且![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】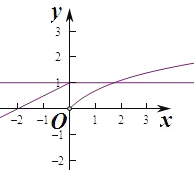
作出函数f(x)的图象如图,
若m<n,且f(m)=f(n),
则当ln(x+1)=1时,得x+1=e,即x=e1,
则满足0<ne1,2<m0,
则ln(n+1)= ![]() m+1,即m=2ln(n+1)2,
m+1,即m=2ln(n+1)2,
则nm=n+22ln(n+1),
设h(n)=n+22ln(n+1),0<ne1
则![]() ,
,
当h′(x)>0得1<ne1,
当h′(x)<0得0<n<1,
即当n=1时,函数h(n)取得最小值h(1)=1+22ln2=32ln2,
当n=0时,h(0)=22ln1=2,
当n=e1时,h(e1)=e1+22ln(e1+1)=1+e2=e1<2,
则32ln2h(n)<2,
即nm的取值范围是[32ln2,2),
本题选择A选项.


科目:高中数学 来源: 题型:
【题目】某公司研发出一款新产品,批量生产前先同时在甲、乙两城市销售30天进行市场调查.调查结果发现:甲城市的日销售量![]() 与天数
与天数![]() 的对应关系服从图①所示的函数关系;乙城市的日销售量
的对应关系服从图①所示的函数关系;乙城市的日销售量![]() 与天数
与天数![]() 的对应关系服从图②所示的函数关系;每件产品的销售利润
的对应关系服从图②所示的函数关系;每件产品的销售利润![]() 与天数
与天数![]() 的对应关系服从图③所示的函数关系,图①是抛物线的一部分.
的对应关系服从图③所示的函数关系,图①是抛物线的一部分.
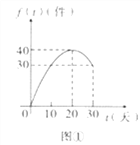
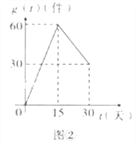

(Ⅰ)设该产品的销售时间为![]() ,日销售量利润为
,日销售量利润为![]() ,求
,求![]() 的解析式;
的解析式;
(Ⅱ)若在![]() 的销售中,日销售利润至少有一天超过
的销售中,日销售利润至少有一天超过![]() 万元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
万元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥S﹣ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: ①异面直线SB与AC所成的角为90°;
②直线SB⊥平面ABC;
③面SBC⊥面SAC;
④点C到平面SAB的距离是 ![]() .
.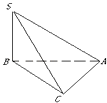
其中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a5=9,a7=13,等比数列{bn}的通项公式bn=2n﹣1 , n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an+bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对某电视剧的喜爱程度,某电视台在甲乙两地随机抽取了8名观众做问卷调查,得分结果如图所示:
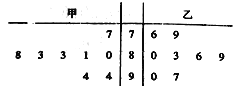
(1)计算甲地被抽取的观众问卷得分的中位数和乙地被抽取的观众问卷得分的平均数;
(2)用频率估计概率,若从乙地的所有观众中再随机抽取4人进行问卷调查,记问卷分数不低于80分的人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
(I)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB= ![]() AC=2
AC=2 ![]() ,AB=BC,求二面角F﹣BC﹣A的余弦值.
,AB=BC,求二面角F﹣BC﹣A的余弦值.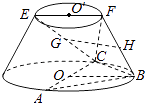
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设离心率为 ![]() 的椭圆
的椭圆![]() 的左、右焦点为
的左、右焦点为![]() , 点P是E上一点,
, 点P是E上一点, ![]() ,
, ![]() 内切圆的半径为
内切圆的半径为 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线![]() 上,A、B在椭圆E上,若矩形ABCD的周长为
上,A、B在椭圆E上,若矩形ABCD的周长为 ![]() , 求直线AB的方程.
, 求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com